Chapter 14 - Frequency Response
The Frequency response of a circuit is the variation in its behavior with change in signal frequency.
Transfer Function
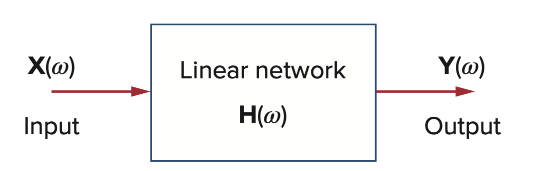
The transfer function
Y and X can either be voltage or current Hence 4 types of transfer function
Voltage gain:
Current gain:
Transfer impedance:
Transfer admittance:
Polynomial expression
N和D分别为由Y和X简化后得到的两个多项式
其中,
其中,
常用s替换jw来避免进行complex algebra,最后再替换回去
Transfer function 实际是由电路的differential equation 进行 Laplace Transform 后得到的式子
Decible Scale
Bel
Used to measure the ratio of two levels of power, called power gain G
Decible - 1/10 of a bel
Assume
正是因为平方的关系,Gain的log前面才是20这个比较奇怪的数字
Bode Plots
Bode plots are semilog plots of the magnitude(in decibles) and phase(in degrees) of a transfer function versus frequency.
semilog plot: 一个坐标轴是log scale,另一个是linear
decibles: 指每格增长10倍,所以是semilog plot
bode plots就是两个图,横坐标都是angular frequency in decibles(
),分别是 和 图像 这两个图分别对应着transfer function
的magnitude 和 phase
使用decible 表示H:
常见的gain
Magnitude H -3 1/2 1 0 1 3 2
Standard Form of Transfer Function
Constant Term -

Zero/Pole at the origin - (
For
For
Generalize 之后,对于

Simple Zero/Pole - (
最简单的情况,
我们用linear approximation来绘制这两个图
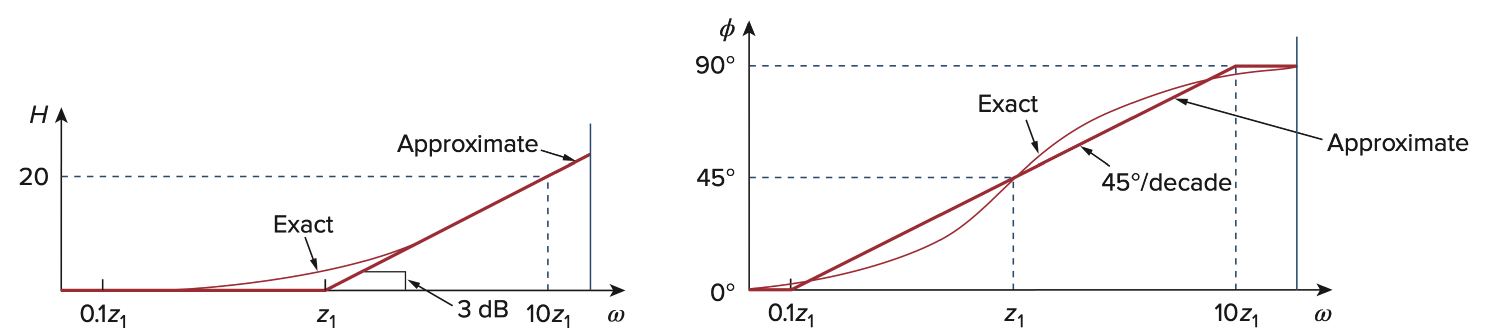
当
Generalize之后,对于double zero(N = 2),或任意N,有

Quadratic Zero/Pole - (
注意,double pole -
有别与quadratic pole,重点就在 damping factor - 上 ?(*具体是什么不知道,长大后在学习)
对于不同的
图像与double zero一样,N = 2, H斜率为40dB/decade,
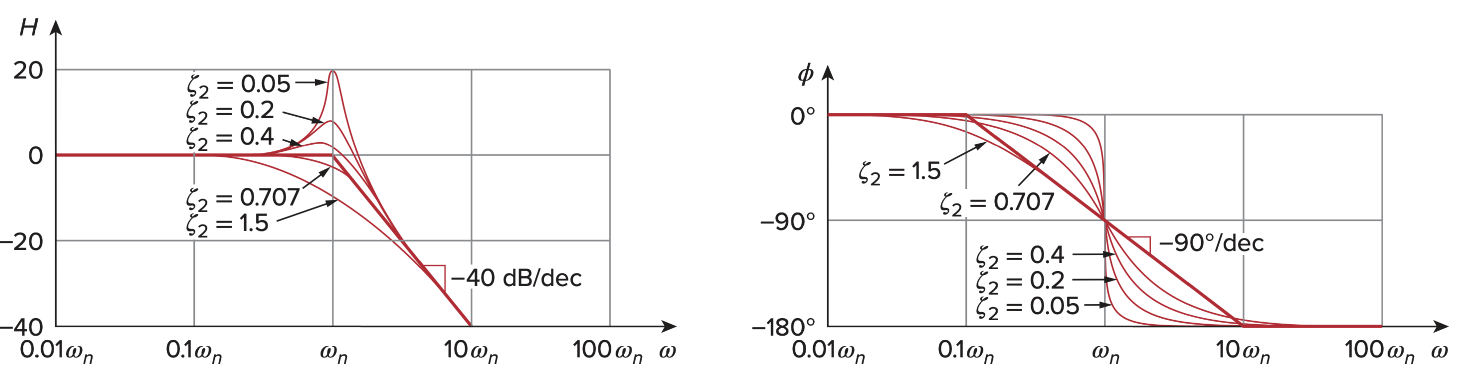
这个是pole的图像,
Zeros cause an increase in slope
Poles cause a decrease
从数学上可以看出来,因为pole在分母上,但为什么会有这种behavior还需要对transfer function有更深入的理解?
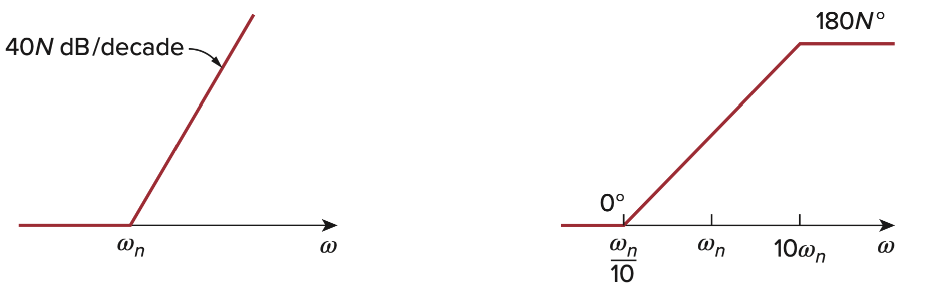
Resonance
Resonance is a conduction in an RLC circuit in which the capacitive and inductive reactances are equal in magnitude, thereby resulting in a purely resistive impedance (The imaginary part of the transfer function is 0)
Resonance occurs in any system that has a compliex conjugate pair of poles.(?)
The frequency that satifisfies the condition
Series Resonance
任何series circuit都可以变成RLC串联的形式
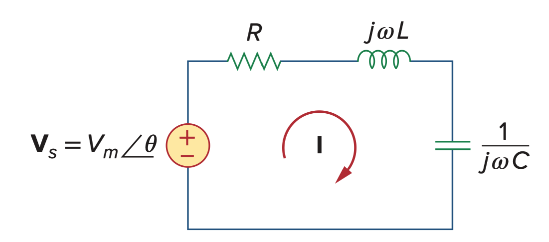
注意频率单位,Hz为频率,弧度为角速度
Half-Power Frequency
The dissipated power is half the maximum value
Average (active) power dissapated by the circuit
active power(P) 指电路中电阻(R)消耗的能量(有功功率)
与之对应的是reactive power(Q) (无功功率)
Apprant Power
在实数域上
当resonance时功率最大,此时
因此,当
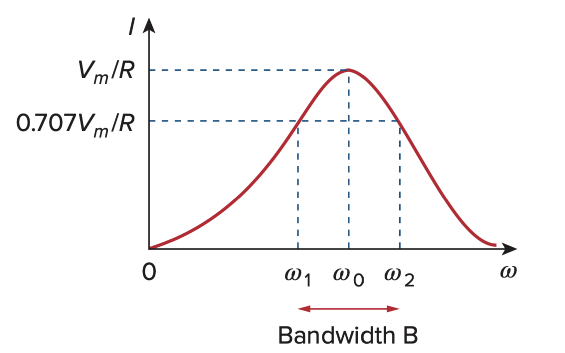
图中的R代表电阻的R,不是当时电路总阻抗的R值
那么电路总阻抗的R值应该变为
求解
resonant frequency is the geometric mean of the half-power frequencies
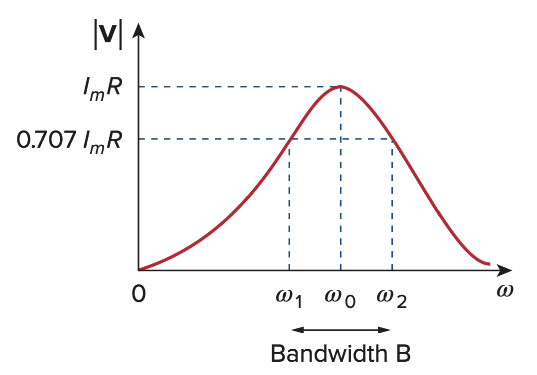
Bandwidth B - difference betwee half-power frequencies
Quality Factor(Q)
Reactive Power也是Q,但此Q非彼Q
The Quality Factor relates the maximum energy stored to the energy dissipated in the circuit per cycle of oscillation at resonance
Peak Energy stored:
Let
带入
因此
Q与B成反比,因此Q越大,selectivity越小
The selectivity of an RLC circuit is the ability of the circuit to respond to a certain frequency and discriminate against all other frequencies.
在谐振电路中,电容和电感上的电压可以远大于输入电压
两个元件上的实际电压都可能大于电源电压
在串联谐振电路中,
(就是之前的 ) 由于电容和电感的特性,电感让电流比电压lead 90,电容让电压比电流lead 90,最后结果就是两个抵消了,电感和电流上电压大小相同,phase相差180度
High-Q circuits
When quality factor

红色和绿色分别代表
橙色是
当
当
可以看到这个电流函数其实是不对称的,是由于我们的Q不够大,可以想象当Q足够大时,
基本对称
Parallel Resonance
一个道理,不过这次改用admittance,之前电压的关系现在变成了电流的关系
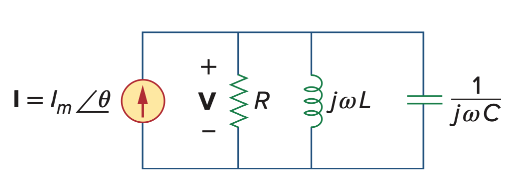
注意,这里根series不一样,C和L互换了位置,因为Y = 1/Z
电感和电容两个构成回路,对整个电路来说像是断路
由于
我们可以只记Q的不同,剩下的用Q来表示
| Characteristic | Series Circuit | Parallel Circuit |
|---|---|---|
| Resonant Frequency( | ||
| Quality factor(Q) | ||
| Bandwidth(B) | ||
| Half-power frequencies( | ||
| For |
Passive Filters
A Filter is a circuit that is designed to pass signals with desired frequencies and reject or attenuate others.
A filter is a passive filter if it consists of only passive elements R, L and C.
A filter is an active filter if it consists of active elements.
Low-pass Filter & High-pass filter
在filter中, cutoff frequency(
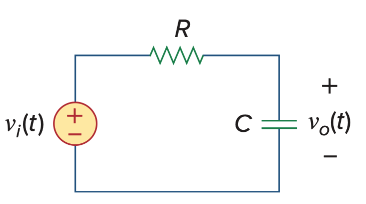
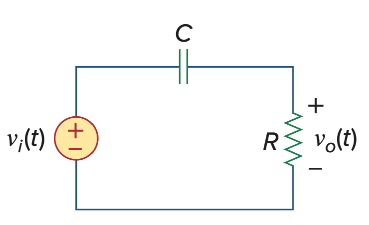
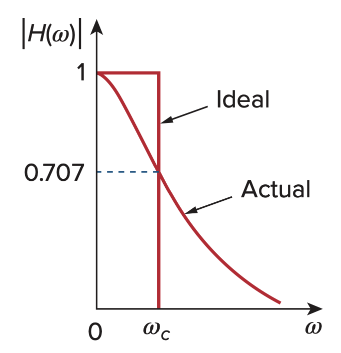
两种filter用的是同一个电路,这个RC电路中,电阻上的电压是高频电压(高频电流流过了capacitor,在电阻产生电压)
电容上是低频电压(低频的信号由于无法跨过电阻在电阻两端产生电压)
Low pass:
High pass:
Band-pass Filter & Band-stop filter
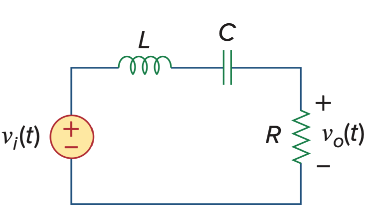
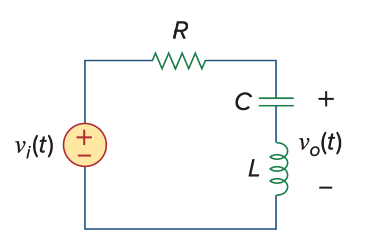
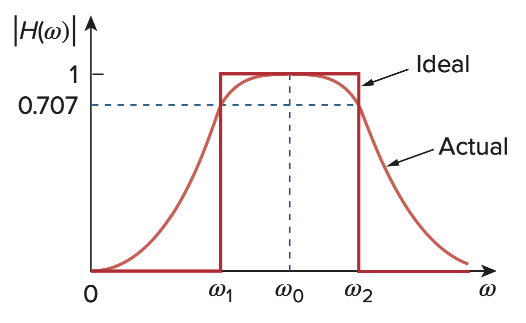
使用resonance circuit,电流的图像刚好符合我们的需求,电阻上的电压是band-pass, 电容和电感上的电压是band-stop
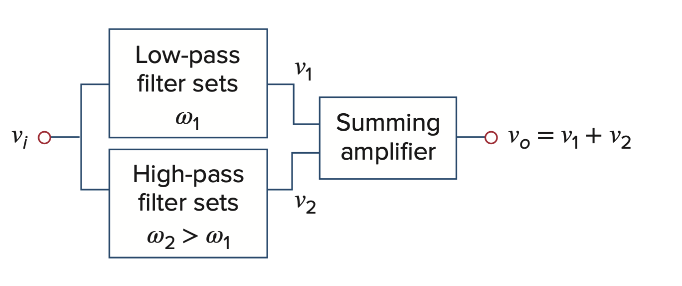
Band-pass 无法使用一个low-pass串联一个high-pass,因为后面的circuit会load前面的circuit,最终结果会与预期不同。下面可以看到是用op amp可以实现电路隔离。事实上,使用active filter的一大好处就是可以不使用电感(占用PCB空间)
| Type of filter | |||
|---|---|---|---|
| Low-pass | 1 | 0 | |
| High-pass | 0 | 1 | |
| Band-pass | 0 | 1 | 0 |
| Band-stop | 1 | 0 | 1 |
在面对一个未知电路时,如果不知道它是什么类型的filter,可以通过对应上面这个table来决定
Active Filters
Active Filter 特性
可以有大于1的gain,向电路中增加能量
不需要电感
passive filter在低频perform poorly
不过Active filters are less reliable and less stable. Pratical limit is about 100kHz, 工作频率要低于次频率。
General first-order active filter (order = number of poles)
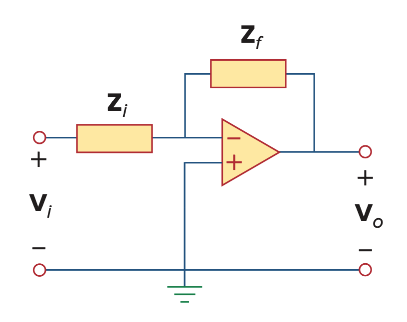
First Order Low-Pass Filter
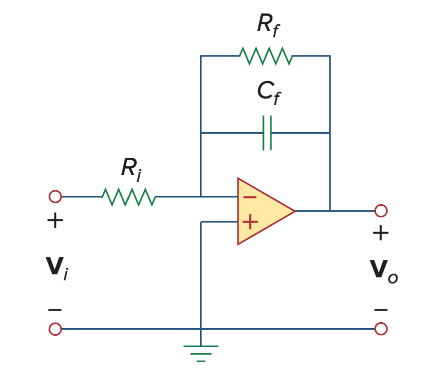
First Order High-Pass Filter
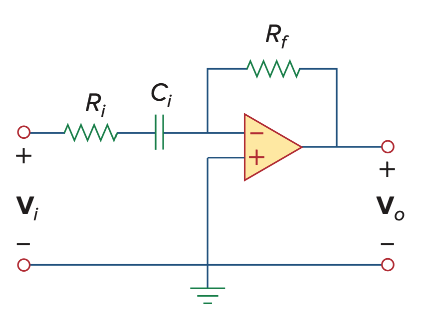
注意,这里不是没有了
的gain,而是无法从分母提出来,但其实当 变大时, 趋向于
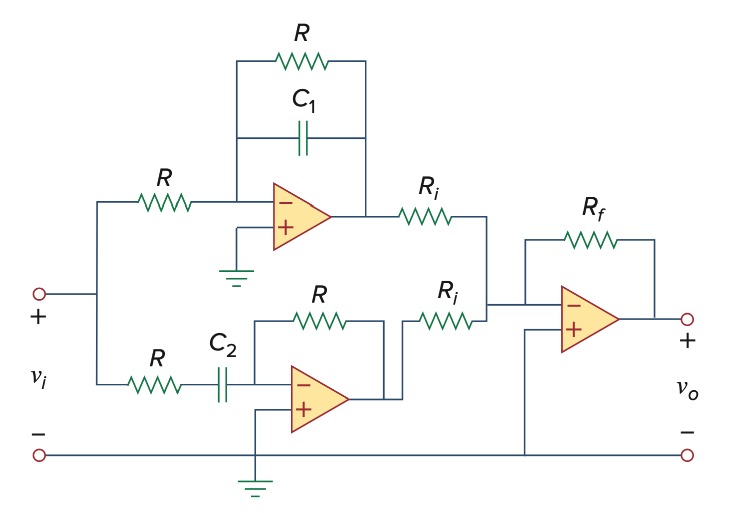
Band-Pass Filter

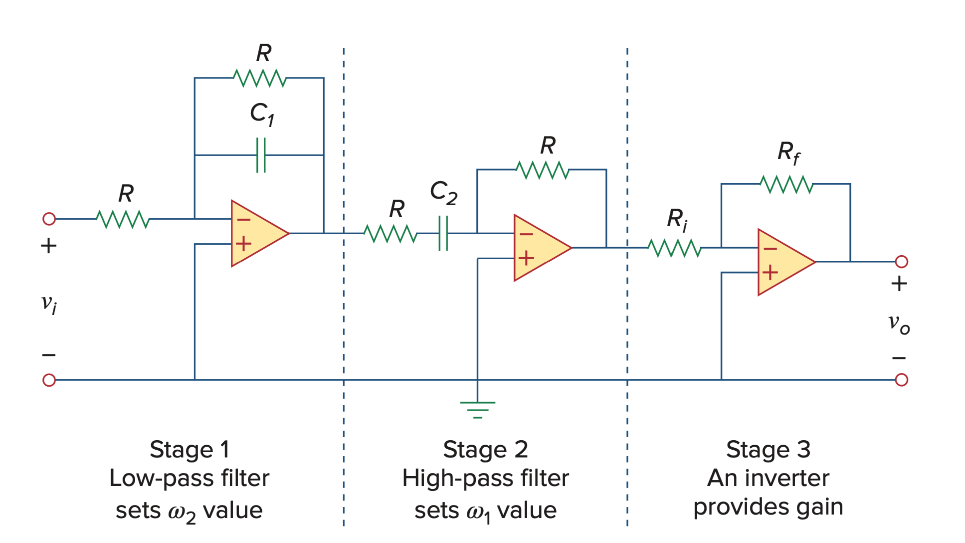
Low-pass section:
High-pass section:
有了这两个,我们就能算剩下的
使用Standard form化简H得到
带入
passband gain :
最后的inverter不是为了invert,而是像图中所说的provde gain。事实上,在经过inverter前,信号是跟原来的phase一样的,只是没有
的gain
Band-Reject Filter (Notch Filter)
在
在
Scaling
Magnitude Scaling is the process of increasing all impedances in a network by a factor, the frequency response remaining unchanged
Frequency Scaling is the process of shifting the frequency response of a network up or down the frequency axis while leaving the impedance the same
| Varible Name | Magnitude Scaling | Frequency Scaling | Scaling Together |
|---|---|---|---|
| Resistor | |||
| Inductor | |||
| Capacitor | |||
| Angular Freq |
When scaling together:
Diodes
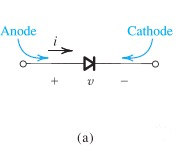
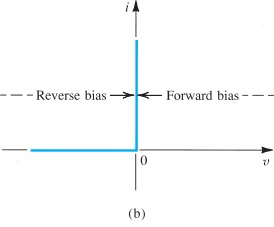
Ideal Diode
名副其实的理想二极管,要么导通(on, turn-on, forward bias),要么不导通(off, turned-off, reverse bias)
Ideal Model 适合快速分析二极管的通断
Junction Diodes
使用pn结制成的二极管通常会有如下i-v characteristic
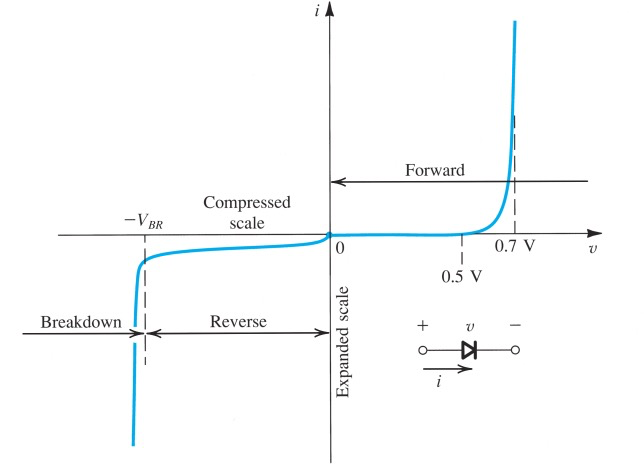
Forward-Bias region
directly proportional to the cross-sectional area of diode For small signal diodes,
is in the order of . It doubles in value for every rise in temperature
k = Boltzmann's constant = 8.62e-5 eV/K T = absolute temperature q = magnitude of electronic charge = 1.6e-19
Usually use the 20 Celcius,
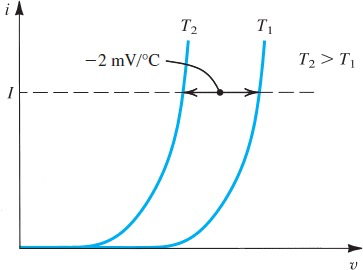
Voltage drop decreases about 2mV per 1 Celcius temparature increase. (可以用来做温度计)
Reverse-Bias Region
沿用上面的公式,在v < 0时,可以近似为
reverse current主要源于leakage effect,受到pn结横截面积影响,但与
reverse current doubles for every
Breakdown Region
二极管的反向击穿,当电流低于Breakdown Voltage
https://www.bilibili.com/video/BV1S34y167Ck/
Avalanche Breakdown 雪崩击穿
电子将共价键中的电子创出来,被创出来的电子又去创其它的,像核裂变一样导致载流子增多
一般用于由较小变化引发较大电流的场景,比如感光器件
Zener Breakdown 齐纳击穿
耗尽层较薄,中间电场较大,电子得到足够能量破坏共价键
一般齐纳击穿所需反向电压较小,
两种击穿都是可逆的,不过雪崩击穿由于电压很大,不控制住电流可能会导致烧掉二极管
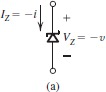
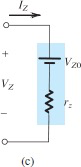
稳压二极管 - Zener Diode
通过zener breakdown来钳位电压,适合小功率负载
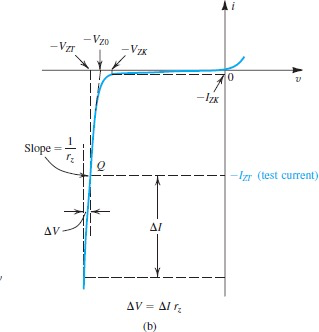
在Q点附近(Q点为测试点,测试电压为
The temperature coefficient of zener voltage
is commonly known as temco, and expressed in
Shunt regulators
regulator circuit appears in parallel(shunt) with the load
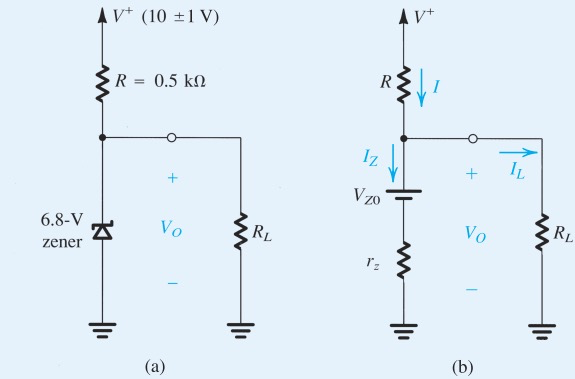
Diode Models
Ideal model - 上面提到了,一般只用来测通断
Exponential Model
当
由于exponential model不是线性的,所以一般用图像法,或者interative analysis来求得方程组的解
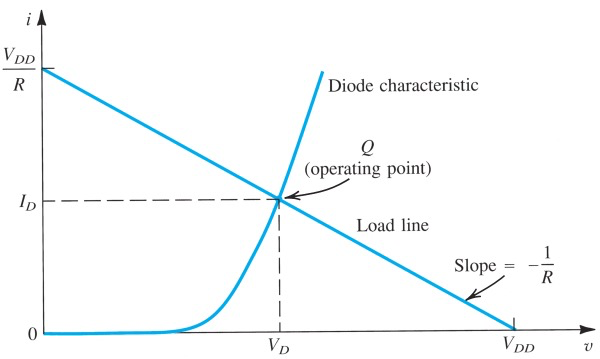
Constant voltage drop model
然而,一般情况下这种分析很耗时,所以观察二极管伏安特性曲线,在
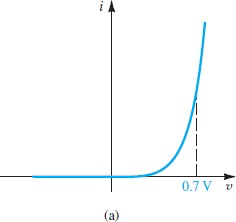
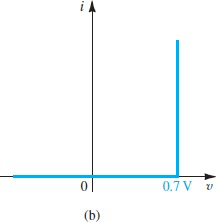
也因为这个性质,可以用二极管来钳位0.7V电压
Small Signal Model
当电路的交流signal很小时,二极管近似工作在线性区域
我们将电压分为直流部分和交流部分,
那么可以近似为二极管在Q点的切线上工作
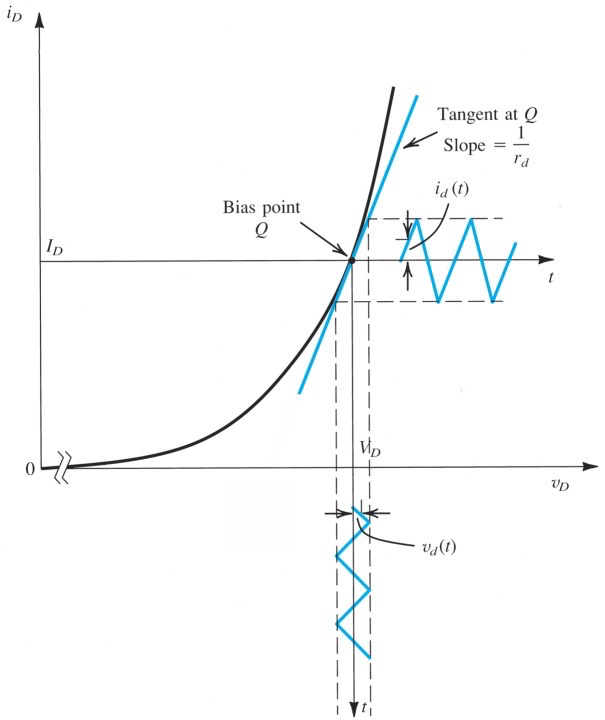
Q点为quiescent point,是只有直流部分时造成的i-v,满足
那么
当
这个叫做small-signal approximation,usueally valid when
此时的等效电阻small-signal resistance

Rectifier Circuits
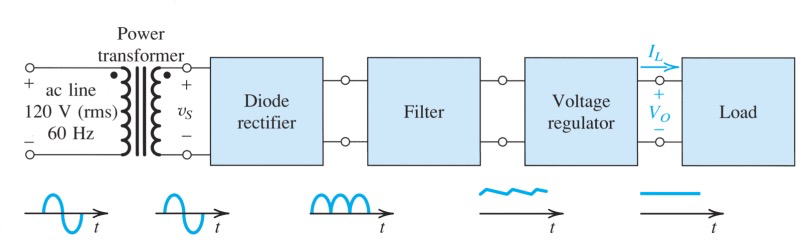
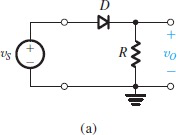
Half-Wave Rectifier
Peak inverse voltage
一般选元器件时选择50% greater than PIV
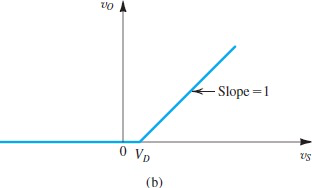
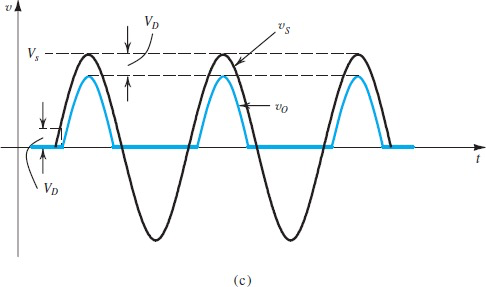
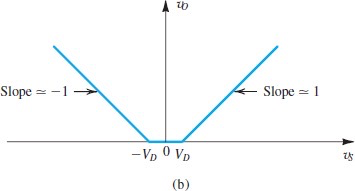
Full-Wave Rectifier
需要center-tapped到变压器线圈中间
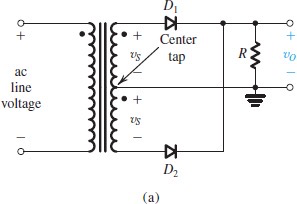
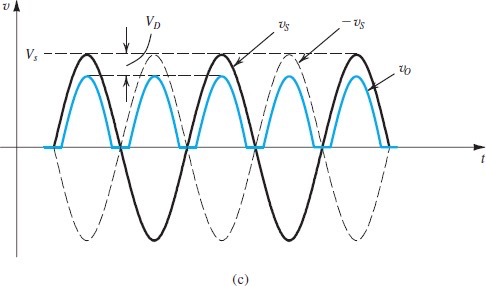
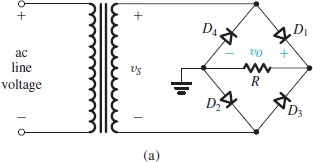
Bridge Rectifier
优势时不用center-tapped到变压器中间,同时相比full-wave只需要一半线圈
缺点是
假设D1, D2导通,那么
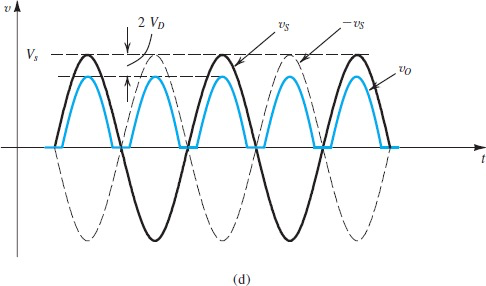
Peak Rectifier
使用一个filter capacitor来将电压维持在最高点
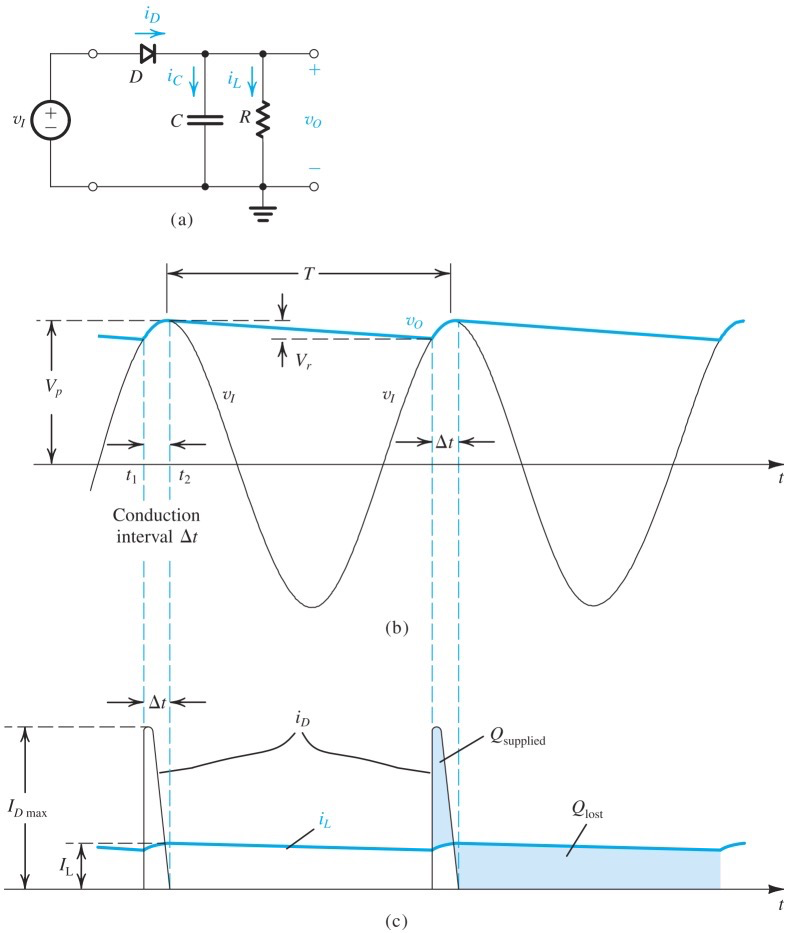
Ripple Voltage
当波形为负时,右半部分构成RC电路,持续放电,因此我们希望
当R = 0时,电路没有负载,电压会一直稳定在Vp
而在这个rectifier里,t = T
因为RC >> T,
Charge
在电容放电时,电流恒定,而放电时间为第一次达到
令充电时间 =
因为充电时间相对T来说很短,
根据电容特性,并且在充电期间也在持续放电(
根据电荷守恒,
根据电路,
而充电最快时应为一开始充电时(假定t=0时在电压最高值,
由上面
使用泰勒展开近似
可以看到当
Full-wave peak rectifier
与half-wave推导过程相同,只不过原来的一周期,现在能充电两次,因此现在的周期是T/2
因此两个公式变为
跟之前的根号项相比为1/2
Peak detector
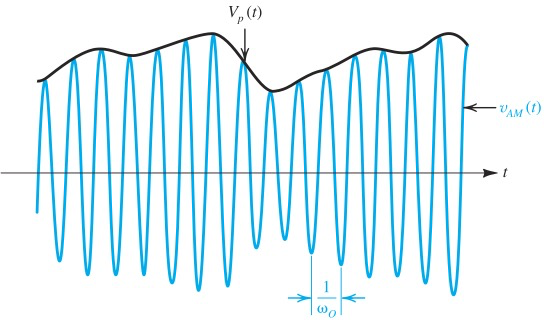
通过相似的电路,可以得到由正弦波携带的信号
这里面正弦波叫做carrier,可以通过不同的频率来区分不同的信道
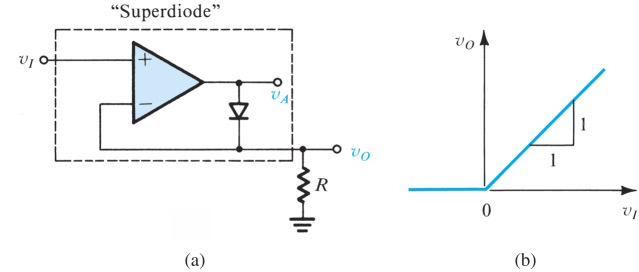
Percision Half-Wave Rectifier - Superdiode
使用一个运放来补上二极管的压降,达到理想二极管的伏安曲线
Other Diode Applications
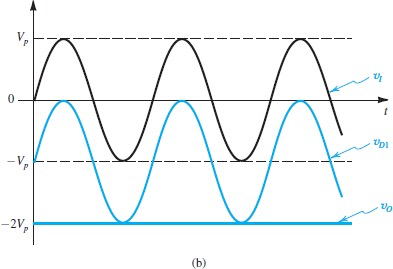
Clamped Capacitor and Bootstrapping (dc restorer)
使用peak rectifier,但取二极管的电压
这样输出电压会是二极管的PIV,而正向导通时会将输出的最低电压拉到0V,因此这个电路能将交流电最低点呀拉高/拉低到0V,使其直流的共模信号为
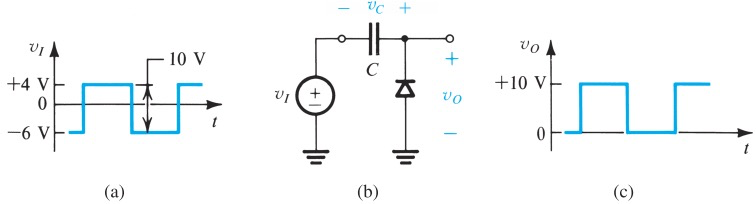
这个图的
产生的就是方波,不是这个电路转换成的方波
这个电路在PWM Pulsewidth Modulation时会被用来将电压拉到0V以上,然后在后面接上一个RC电路来得到平均电压。
Bootstrapping Circuit
在输出接上一个电源,这样可以把低压拉到任意位置

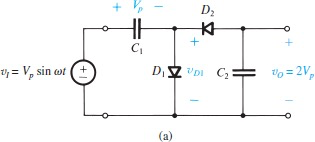
Voltage Doubler
前半部分是clamped capacitor,后面接上一个peak rectifier,可以使输出的直流电压为
Varactors
在反向区域由于pn结的特性,导致二极管有一定的电容
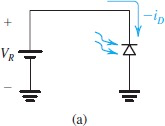
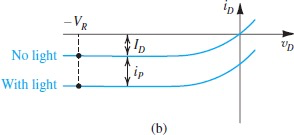
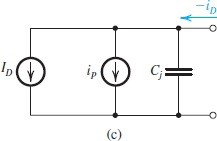
Photodiodes
在reverse bias状态下工作。当受到光的刺激时,电子获得能量,P区和N区会产生新的电子-空穴对,使得区域少子浓度增加。而少子可以通过耗尽层,导致产生少量的漏电流。
The responsivity R is the reverse current produced per watt of incident light power
在黑暗条件下,会有一个最小漏电流dark current
不同材质的半导体产生电子-空穴对的能量需求不同,因此会吸收不同波长的光(不同颜色的感光)。通常情况下,direct band gap semiconductors对光更敏感,相比于indirect band gap semiconductors可以用更细的耗尽层来感光(感光时间也更短)。
利用雪崩击穿的photodiodes对光线十分敏感。Biased around their reverse breakdown voltage,因此一个光子足以引发雪崩击穿,产生大量电流。
如果不在reverse bias下工作,那么photodiodes就是太阳能板,受到光照会产生电压
LED
电子从导带落回到价带时会产生能级跃迁,使用不同的本征半导体材料代替硅可以让改变这个能量的大小,也可以让这个过程释放光子(direct band gap semiconductors)而不是热能(indirect band gap semiconductors,电子在落回空穴时会有中间态)
由于材料变化,二极管的压降也随材质改变,光的波长越短,需要能量越多
红色 GaP LED压降1.8V,蓝色 GaIn LED压降2.5-4.0V
归根结底LED是二极管,所以使用时一定要加一个限流电阻防止电流过大(一般commerical LED会有内置电阻)
MOSFETS
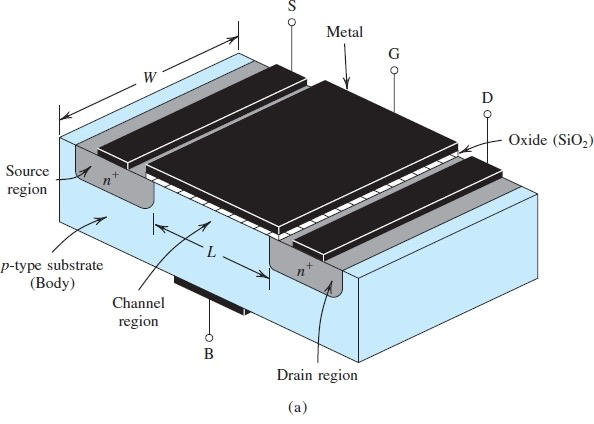
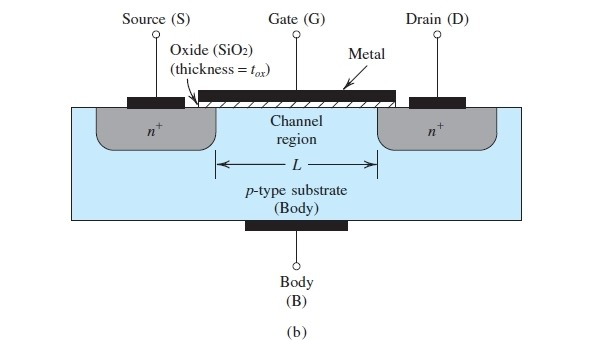
结构如图所示
Operation with Zero Gate voltage
正常情况下,Drain 与 Source之间相当于串联了两个pn结二极管,方向相反,因此无法导通(
Creating a Channel for current flow
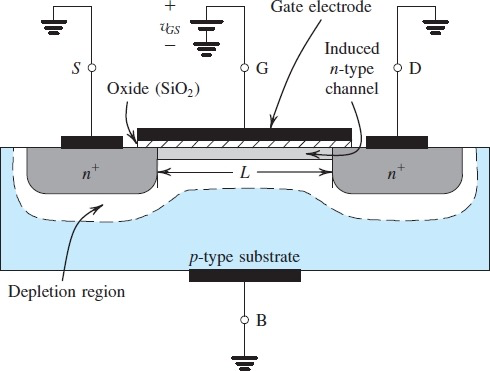
当在G端加上电压后,电子会聚集在氧化物下面,形成一条n沟道。由于n沟道本身导电,此时Drain 与 Source导通
通常使用二极管时会将B和S连接到一起,或者一起接地,因此通常用
来替换Gate和Body之间的电压 由于制作芯片时有时无法做到这点,也有专门的公式来用来校准由于B和S电压差造成的误差(Body Effect)
Gate部分构成平行板电容器。刚刚能产生N沟道的电压叫做threshold voltage
电容器两端的电荷
的permittivity
W, L - 沟道的长度和宽度
当
Small
我们想要计算此时从Drain 流向 Source 的电流
i = electron density on channel surface * drift velocity
electron density:
drift velocity:
conductance:
我们定义process transconductance parameter
我们在定义MOSFET transconductance parameter
因此
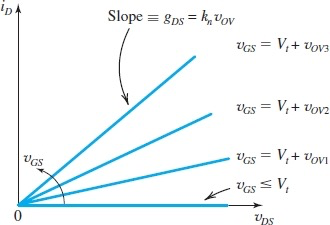
以上推导全部仅限于
足够小的情况,形成的n沟道上的电子可以看作均匀排布,下面推导不够小时发生的情况
When
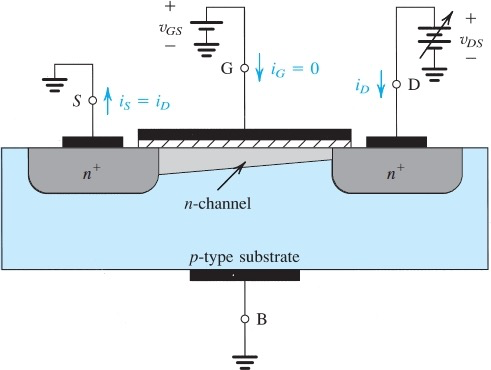
当
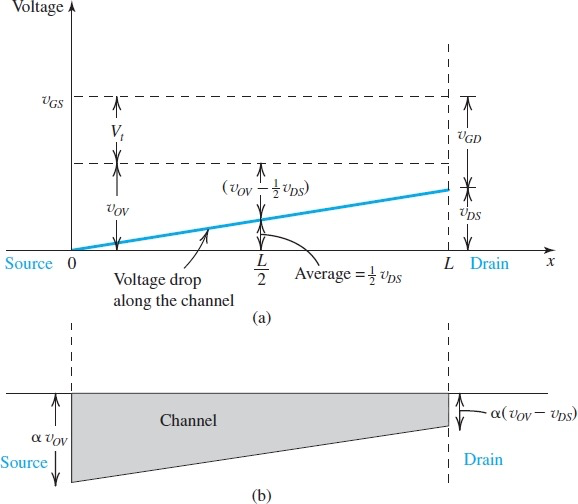
变窄后channel中的电子数量也相应变少,可以从上图看出,channel的面积代表电子的多少。
我们可以用一个更窄的沟道来平替这个梯形沟道,等价的长方形沟道为
我们将新的
可以看到伏安特性实际时一个二次函数
Channel Pinch off and Current Saturation - 夹断
还是上面的图,可以看到当
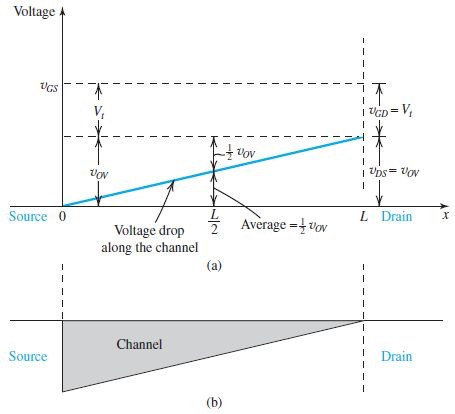
我们称此状态为saturation region(saturation mode of operation),相对应的,未夹断时叫做triode region,从原先晶体管时期得名
The voltage at which saturation occurs
diode connected mosfet - 指在电路中直接将Drain和Gate短接的MOSFET总是在Saturation region,因为
saturation的条件也可以改成
代入之前的公式可以得到此时
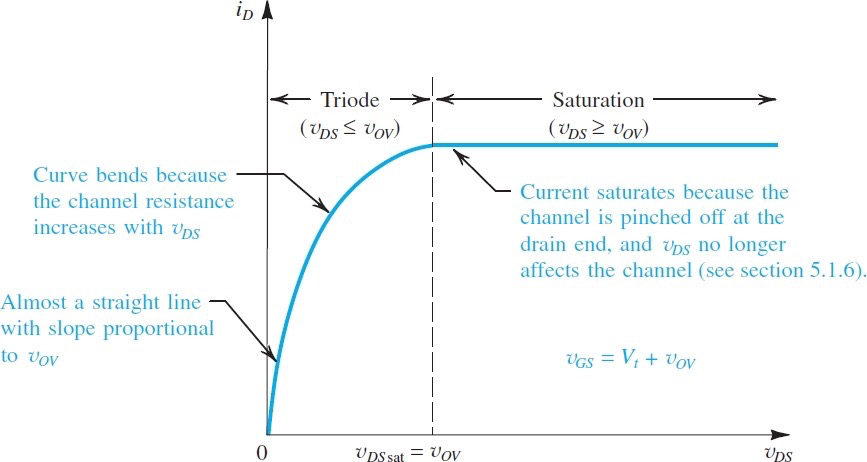
Channel Length Modulation
通常我们都忽略这个效应,assume
但实际上,继续加压会导致channel末端远离Drain
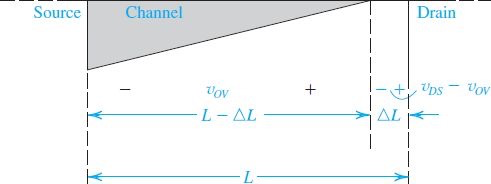
多余的电压被
之前的saturation时电流公式可以看到,
因此
与 真的是线性相关吗?
我们用
令
因此实际的i-v在saturation region会有一个等效电阻
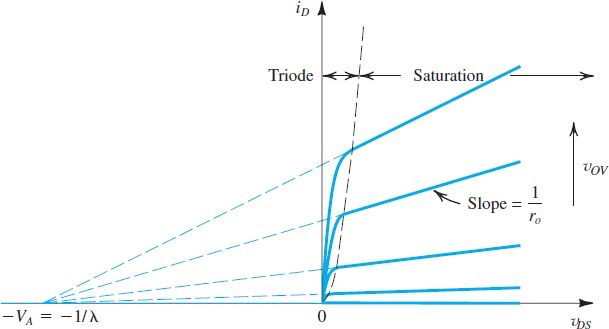
我们一如一个电压
因此
Early是人名
因此,saturation region的large-signal quivlant circuit为:(左为不考虑,右边为考虑后)
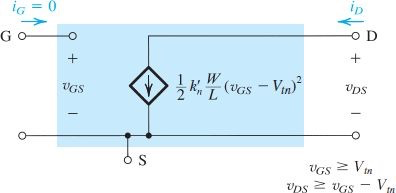
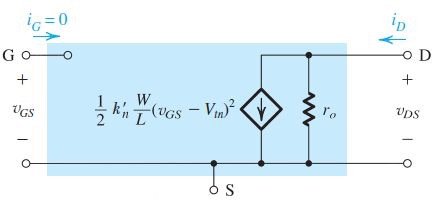
NMOS - n-Channel MOSFET 总结
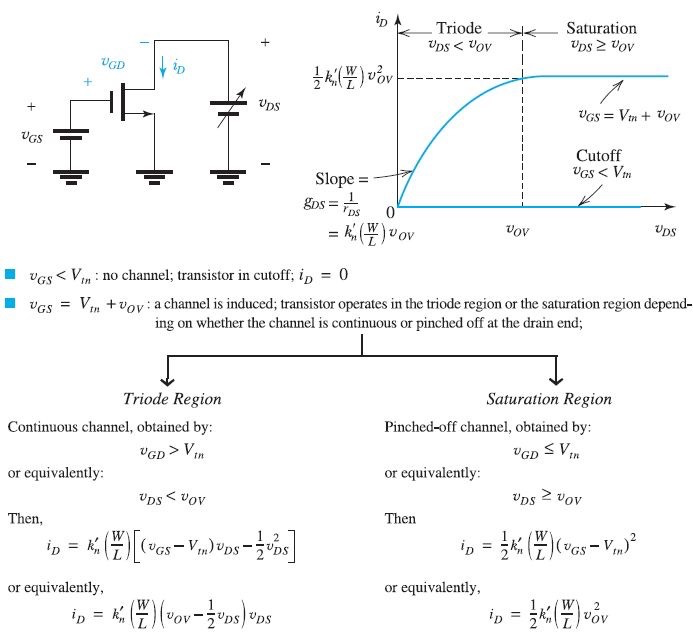
PMOS - p-Channel MOSFET
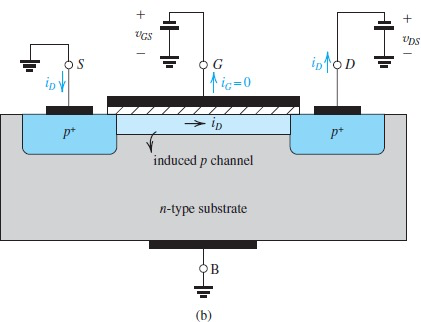
跟n沟道类似,不过全部反过来
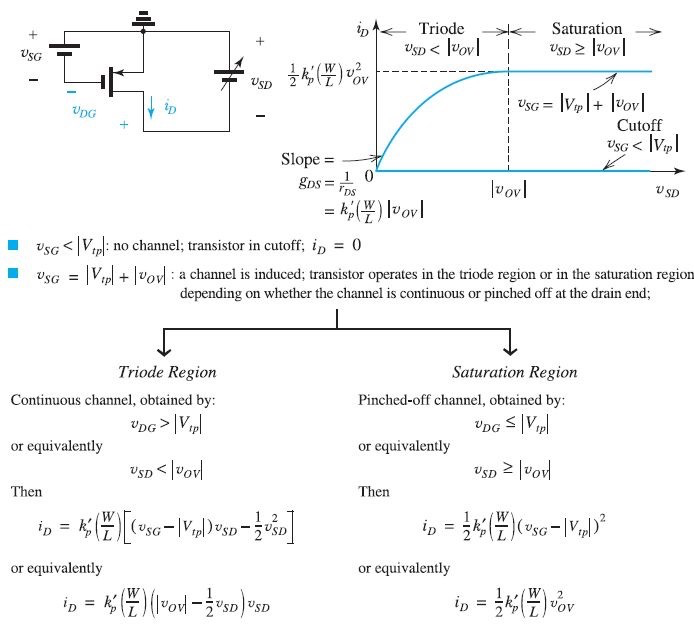
CMOS - Complementary MOS
在同一片硅片上蚀刻出NMOS和PMOS两种MOSFET,在CMOS digital circuit 中很实用
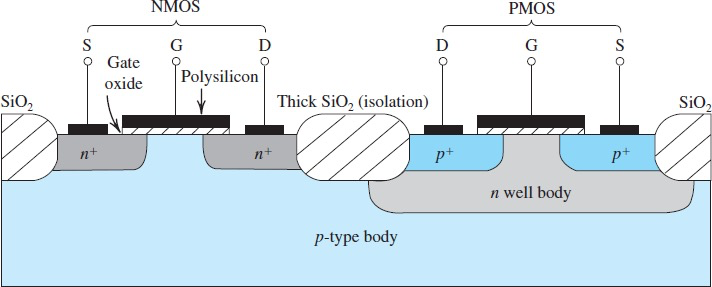
Technology Scaling
每代新的制造科技都会对CMOS工艺产生影响
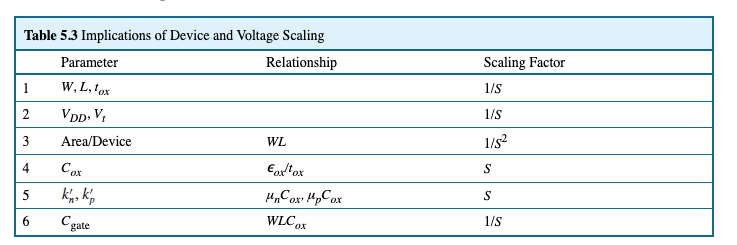
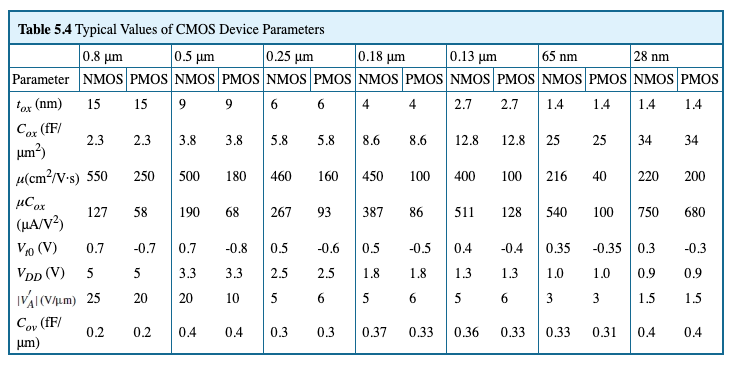
一开始是通过降低厚度( )的方式增大的,到最新的科技 无法继续降低了(漏电),因此换了新的材料 PMOS与NMOS的
减少速度并不相同,最新的科技让两个更接近
由于更短的沟道,channel length modulation更明显,并且有velocity saturation phenomenon,当电场强到一定程度后,电流达到最大值。
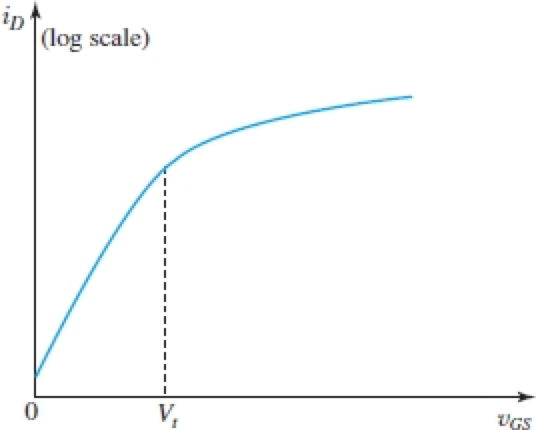
同时,由于更短的沟道和更低的threshold voltage,MOS管会有Leakage current,叫做subthreshold condition
Breakdown
Weak avalanche: 一般发生在10V以上
Punch-through: D端上的电压过大导致耗尽层直接达到S,电流会突然增加,但不会造成permanent damage
静电击穿:发生在金属氧化物的G极,电流过大会击穿电容,导致永久损坏,一般用二极管钳位G极电压,并导出多余电压
由于以上集中breakdown,MOSFET虽然体积小,但不适合高压环境,所以有了BJT
Body Effect
从上面的CMOS图可以看出来,当我们电路需要好多层的MOSFET做逻辑门时,无法让每个MOS的S与B链接。一般B会链接到最低电压的S级(最后一级MOSFET)这会导致对于前面的MOSFET 的
- Threshold voltage when
- physical parameter, typically
- fabrication-process parameter, ,一般为 q = 1.6e-19 C,
- doping concentration, - permittivity of silicon
Depletion-Type MOSFET
正常情况下导通,当施加反向电压时,电容将电子推离n channel,截断电流
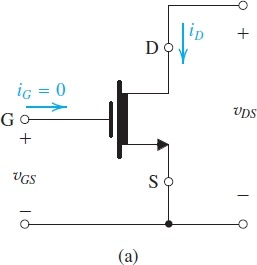
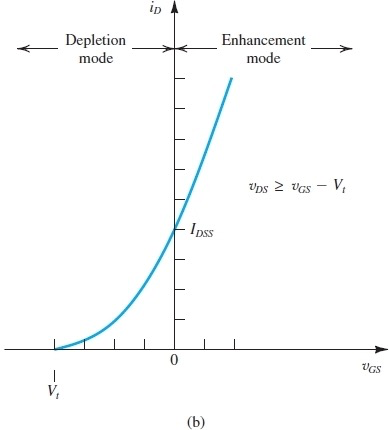
MOSFET Amplifier
原理是让三极管工作在saturation模式下,此模式下
因此transistor is basically a transconductance amplifier - amplifer whose input signal is voltage, output signal is current
通过在DS上串一个电阻
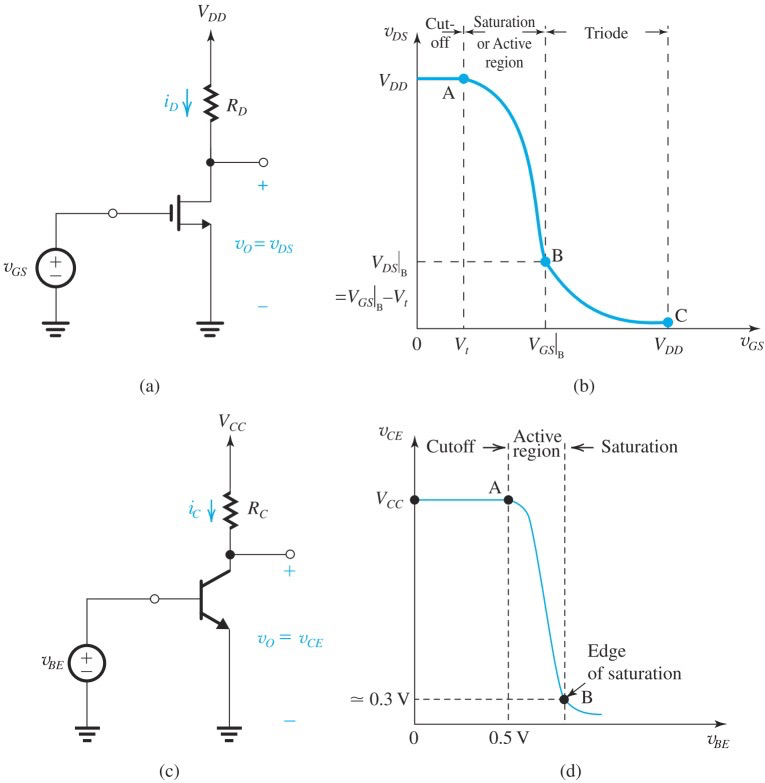
Voltage-Transfer Characteristic(VTC)
VTC就是
上图中已经有了一个charasteric。在satuation region,代入
因此是反过来的二次函数。B点是曲线斜率开始弯折的点,也是saturation与triode的分界点,可以求出它的坐标
这个点上,
由于电压不为负,因此
Obtaining Linear Amplification by Biasing the Transistor
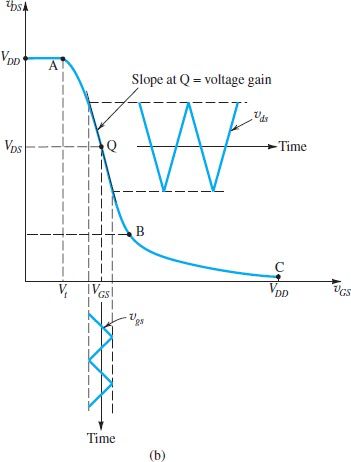
我们在AB之间选择一点Q,叫做bias point/operation point/quiescent point,我们将输入电压分为直流和交流两部分
当
因此
但是在B点,只有B点左侧的增益大,B点右侧进入triode region,不再有相同的VTC,因此选择Q点时应该尽量靠近B点同时预留出足够的Signal Swing的空间。当swing的空间不够大时,我们称它没有sufficient "legroom"
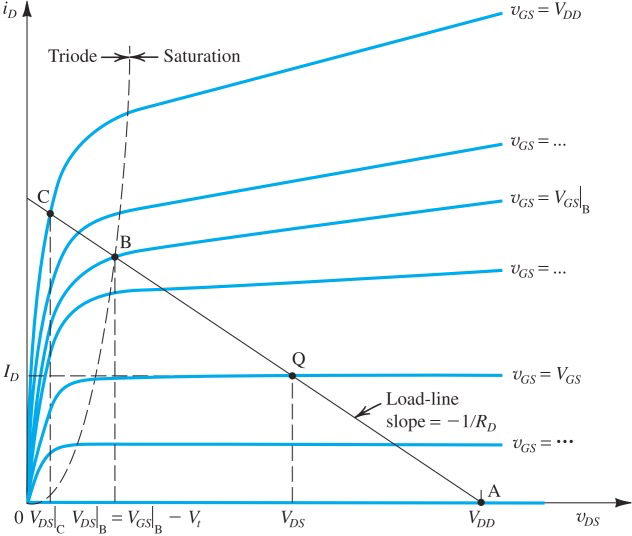
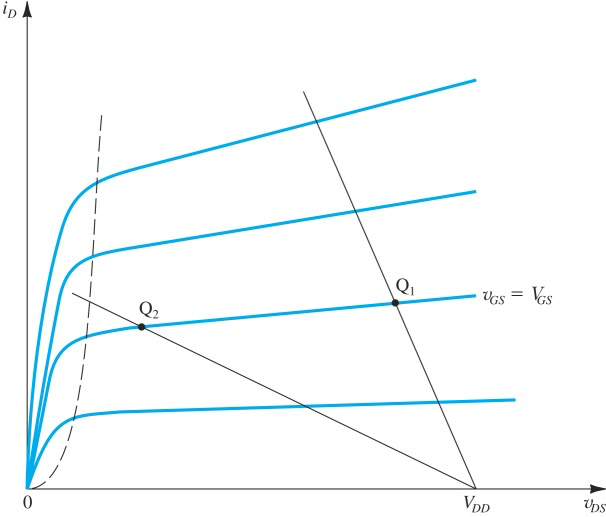
另一种方式来看VTC,跟横轴重合的线是
不同的
取值会改变load line的斜率,这条load line跟不同 的线的交点构成VTC
可以看到
Small Signal Operation and Models
从上面的analysis继续,
第一项是直流component
当
此时
注意这里
用的大写,是dc bias得到的直流电压,这里的证明跟之前求的其实是一回事,不过这次变相证明了小电流条件 从结果来看与我们想要的相符 - 用dc bias控制amplifier gain,小电流模型要的
相当于指之前说的电压输入的要离Q近可能近
关于
首先就是上面的
从之前的
带回第一个式子
高下立判:给定bias current,
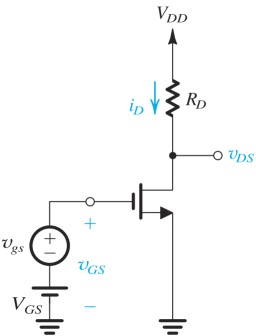
Small signal equivlant model
Hybird-π equvialent model(名字从BJT来的)
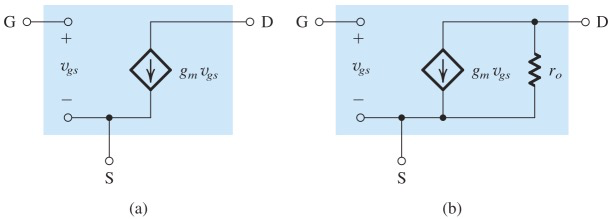
T-model
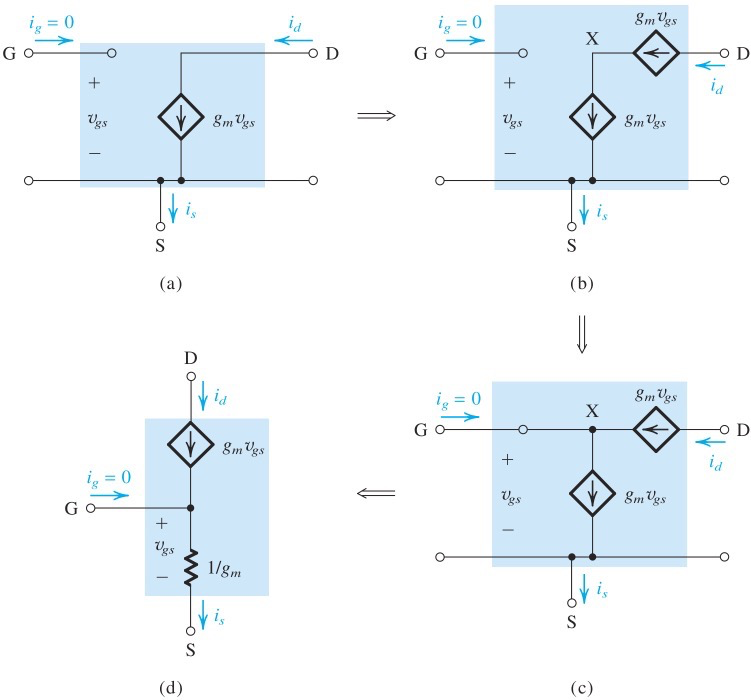
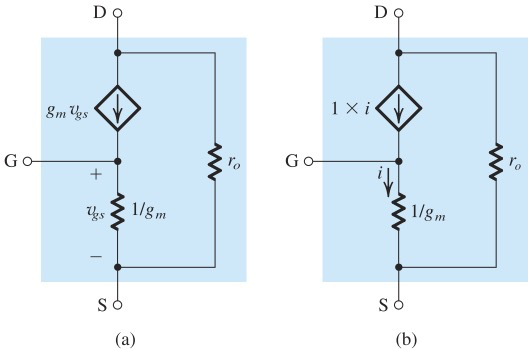
左侧是将Hybrid-π model转化成T model的过程,转化时保证了
当S级接电阻时,直接上T model,这样可以将等效电阻跟Rs串联在一起处理
Modelling Body effect
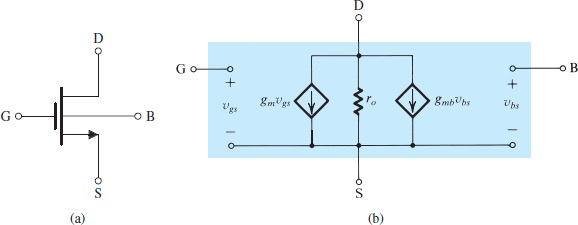
一般在纸笔计算阶段忽视掉
由于
Back transconductance =
这部分的证明不是书上不是很详细?只说了
depends on through the dependence of on ,偏微分后好像是这个答案,但这句话不是很理解?
Basic Configurations
Characterizing Amplifiers
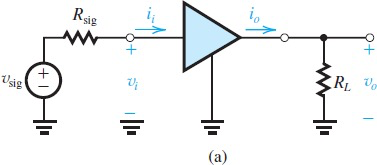
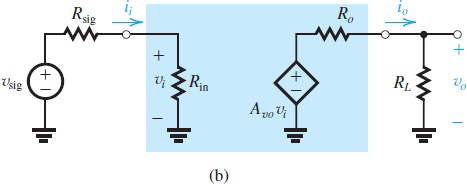
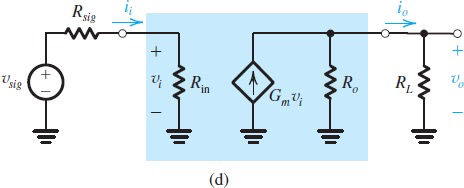
Characterization of amplifier as a functional block,下面是两种变形
Common Source
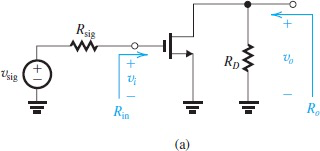
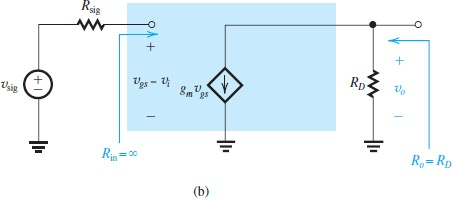
优势:输入阻抗极高
劣势:输出阻抗跟放大倍率挂钩,降低输出阻抗会导致放大倍率降低
在高频下表现不佳,一般将CS 和 CG一起使用
CS with a Source Resistance
https://www.bilibili.com/video/BV1rR4y1w7j9/?spm_id_from=..0.0
在Source的一个电阻可以起到negative-feedback的作用
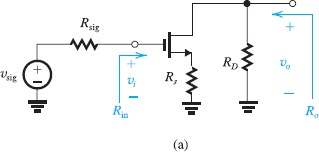
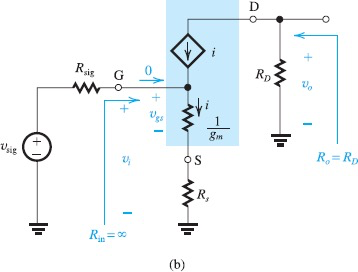
当Source端接有电阻时,无脑上T model
单看
首先,电流源的电流是不变的
注意,
可以看到,对比没有
但是由于
因为
何以见得negative feedback?
从另一个角度来看,当
增加时, 当电流(假如受到轻微扰动)变大时,
减小,导致 变小回去 当电流减小时,
增大,让 再次变大 一个类似运放negative feedback loop的方式将输出卡在它该在的位置上a
后面bias里面有对于
如何降低温度对MOSFET的影响的讨论 更细节的分析在S&S Ch11
从上面的gain的function
Voltage gain from gate to drain = - Total resistance on Drain / Total resistance in source
这个公式对CS amplifier都适用
需要注意的是虽然T-model中的v_sig 有一个 r_sig分压,但实际上那里是虚短
,
Common Gate
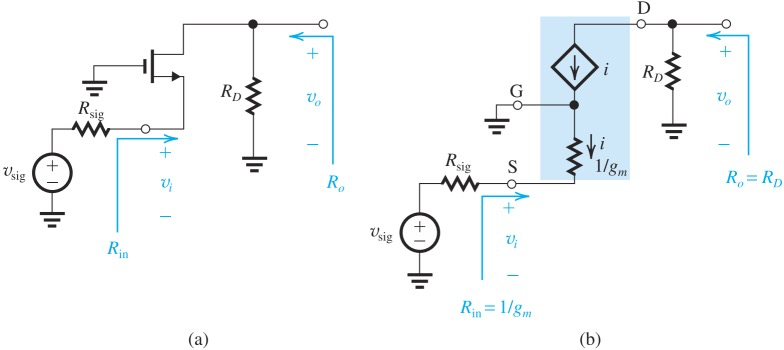
可以通过虚短的性质判断
注意
电阻中电流实际流向时从下到上
除了正负号不同外,gain的表达式跟CS一致, gain = Total resistance on Drain / Total resistance on Source
当接上Load电阻
CG的特性时
通常将CG和CS合起来使用互相弥补短板
Common Drain (source follower)
The need for source follower
一般我们进行信号处理时要进行阻抗匹配,通常是输入电阻尽可能大,输出电阻尽可能小,这样电路的接受能力和驱动能力都会提升。然而,当无法实现时,可以通过source follower来解耦
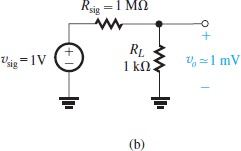
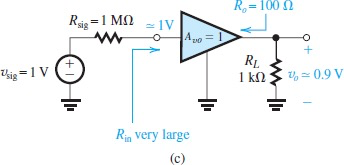
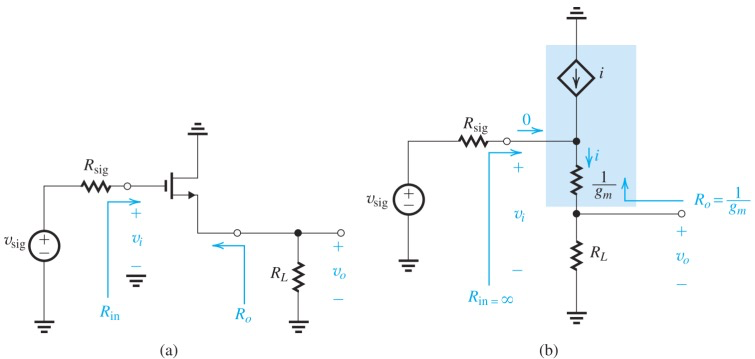
从电路可以看出来,整个amplifier是一个voltage divider
根据定义,
当输入为0时,
因为输入电阻无穷大,
Output Resistance
对于source端没有电阻的amplifier,添加
但对于CS with source resister 和CG来说,添加
nevertheless,在analysis中,
Biasing
最直球的方法就是给
对于制造出的三极管,
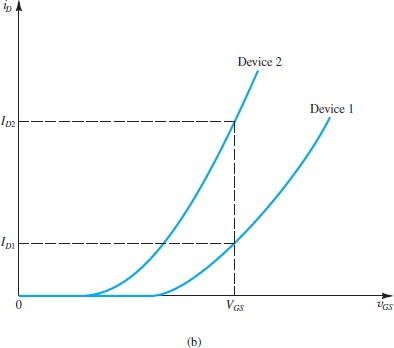
因此,我们用上之前说到的
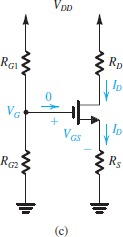
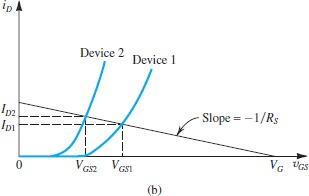
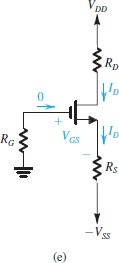
有了这个
因此,实际的工作电流时两个公式的交点
可以从图像中看到,如果两个元器件
如果有两个电源,我们可以使用第三幅图的alternative solution
Drain-to-Gate Feedback Resistor
另一种方式也可以做出feedback,使用一个
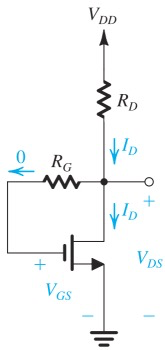
Discrete Circuit Amplifiers
通常设计amplifier时我们先实现dc bias,然后用容量较大的电容隔离直流信号,加入交流部分。这种方式设计的叫做 capacitively coupled amplifiers
这也是小电流模型与dc bias 模型有区别的核心
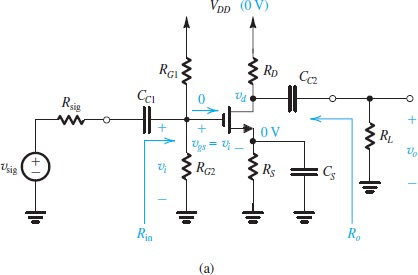
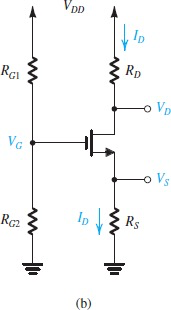
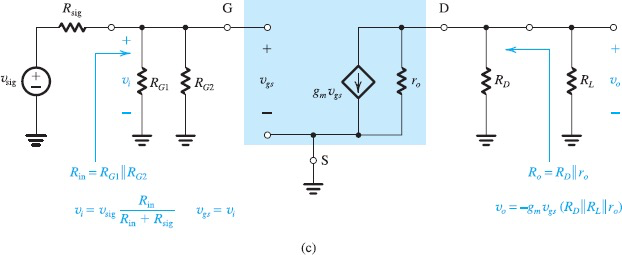
Amplifier Frequency Response
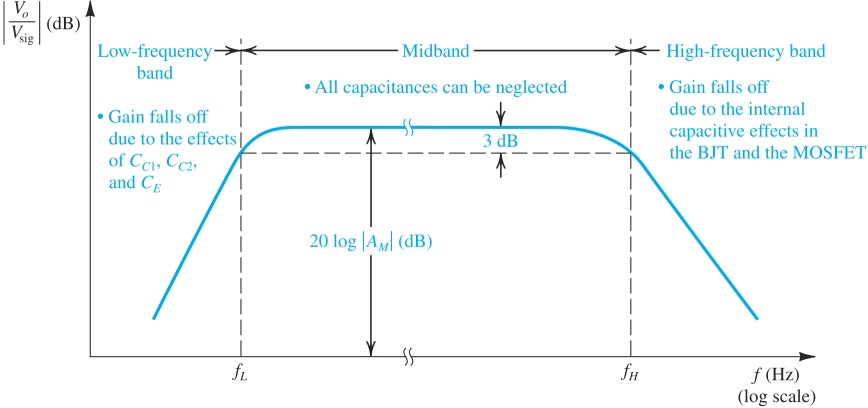
amplifier bandwith:
由于一般频率都是log scale,
在amplifier设计时,一般最大频率(BW)与gain 是一个trade off,两个一般不能同时增大,因此有了一个参数 gain-bandwidth product
CMOS Digital Logic Circuits
Combinational Circuits: The output at any time is a function only of the values of input signals at that time. These circuits do not have memory and do not employ feedback.
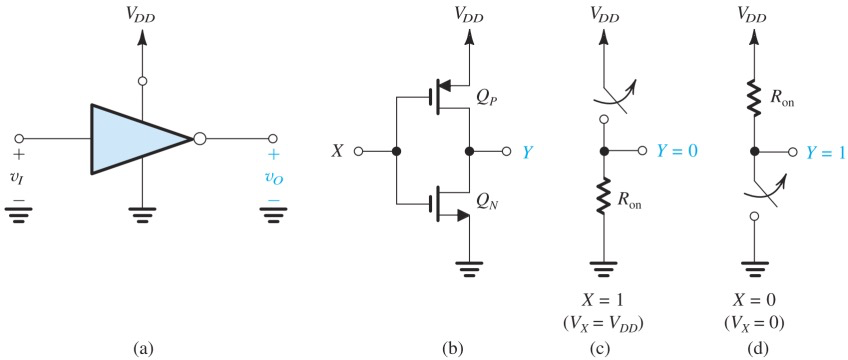
如图为一个inverter CMOS电路图,由此引出General Structure of CMOS logic
PMOS可以当作active low的开关,NMOS当作active high的开关
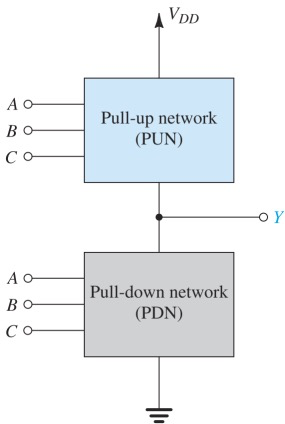
Pull-up network 由 PMOS pull-up transistor 构成
Pull-down network 由 NMOS pull-down transistor 构成
为什么不能反过来或者混用?猜测是反过来的话无法invert,而如果混用则制作工艺太复杂
有了这个inverter之后任何电路都能实现,但如果反过来无法invert那么很多功能实现不了(猜测)?
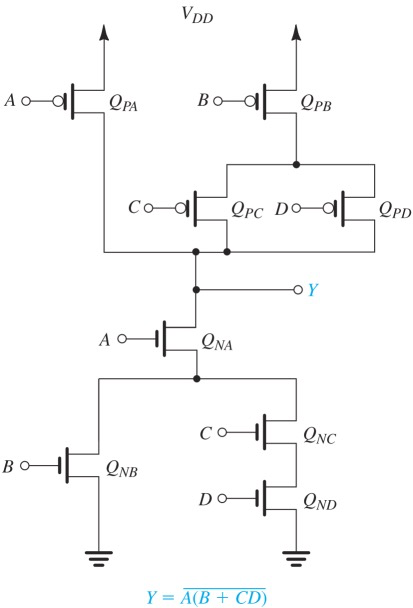
一个CMOS电路例子,Gate上有个圆圈的代表是PMOS(active low)
可以看到,上下是dual circuit(上面的并联是下面的串联,下面的串联是上面的并联)
上半部分实现的是
PUN 使用的是PMOS,因此所有的信号都必须是取反的形式,上面这个就是
PDN使用的是NMOS,因此所有信号都是正的形式,但最终结果是
有些时候无法将function化简为只含有正信号或只含有负信号的形式,比如XOR,
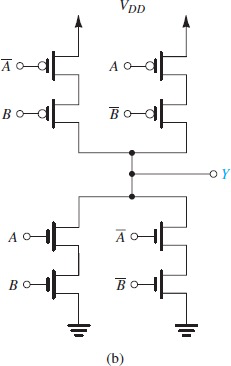
解决方式是将信号前面加上普通的inverter,这样上面这个图实际需要8 + 2*2 = 12个MOSFET(每个负的信号需要多两个)
上面电路中,PDN和PUN严格意义上不是dual circuit(不是串联换并联,并联换串联),但这两个在逻辑上是等价的,并且严格意义上的dual circuit也是可以用的,只是这里没有用
VTC of MOSFET inverter
先来看只有一个MOSFET组成的inverter
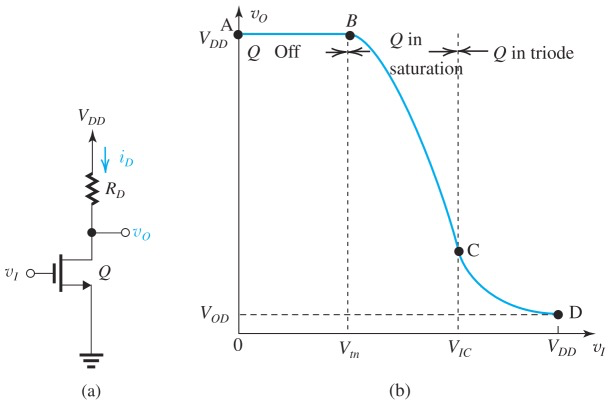
熟悉的VTC,跟之前MOSFET amplifier的完全一致
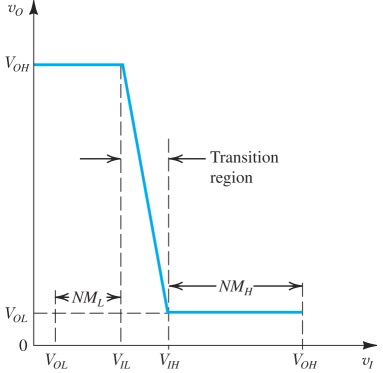
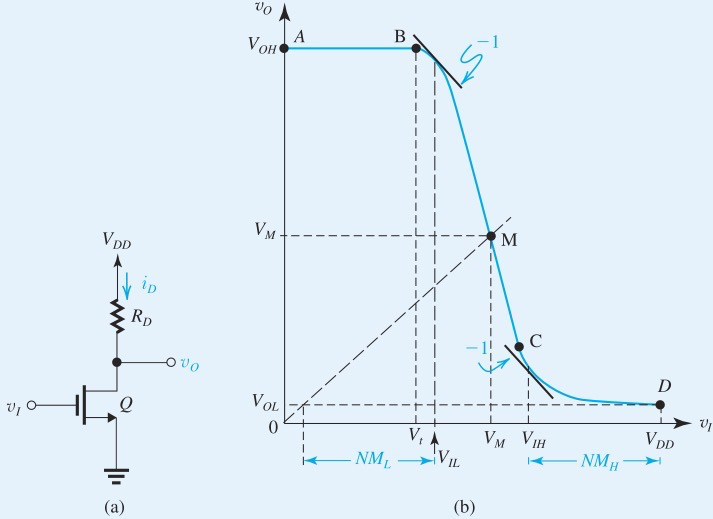
Noise margin for low input不是直接
,因为在数字电路中输入电压往往来自另一个cmos network
在右图表示了一些比较关键的点
两个Slope = -1的点划分出来了transistion region,注意transistion region并不是saturation region,它还包括了一部分triode region(saturation region是严格递减的二次函数)
M是
图中展示的叫做Resistively Loaded MOS Inverter
从之前amplifier的公式可以知道,
因此,在transition region,如果想让线路更陡,我们需要更大的
由于在集成电路上放置大电阻很消耗芯片面积,因此往往用一个Gate接地的PMOS来代替,叫做Pseudo-NMOS inverter
可以在后面分析CMOS的
图中看出来,如果是电阻的话,将会是一条直线与NMOS operation curve的交点,而PMOS则是一条曲线,通过选择不同型号的PMOS即可替代电阻 为了使
足够小, 斜率要很小才能在很早的地方与curve相交
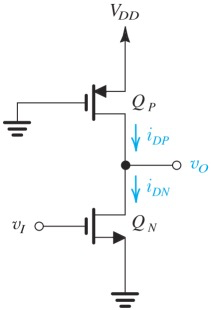
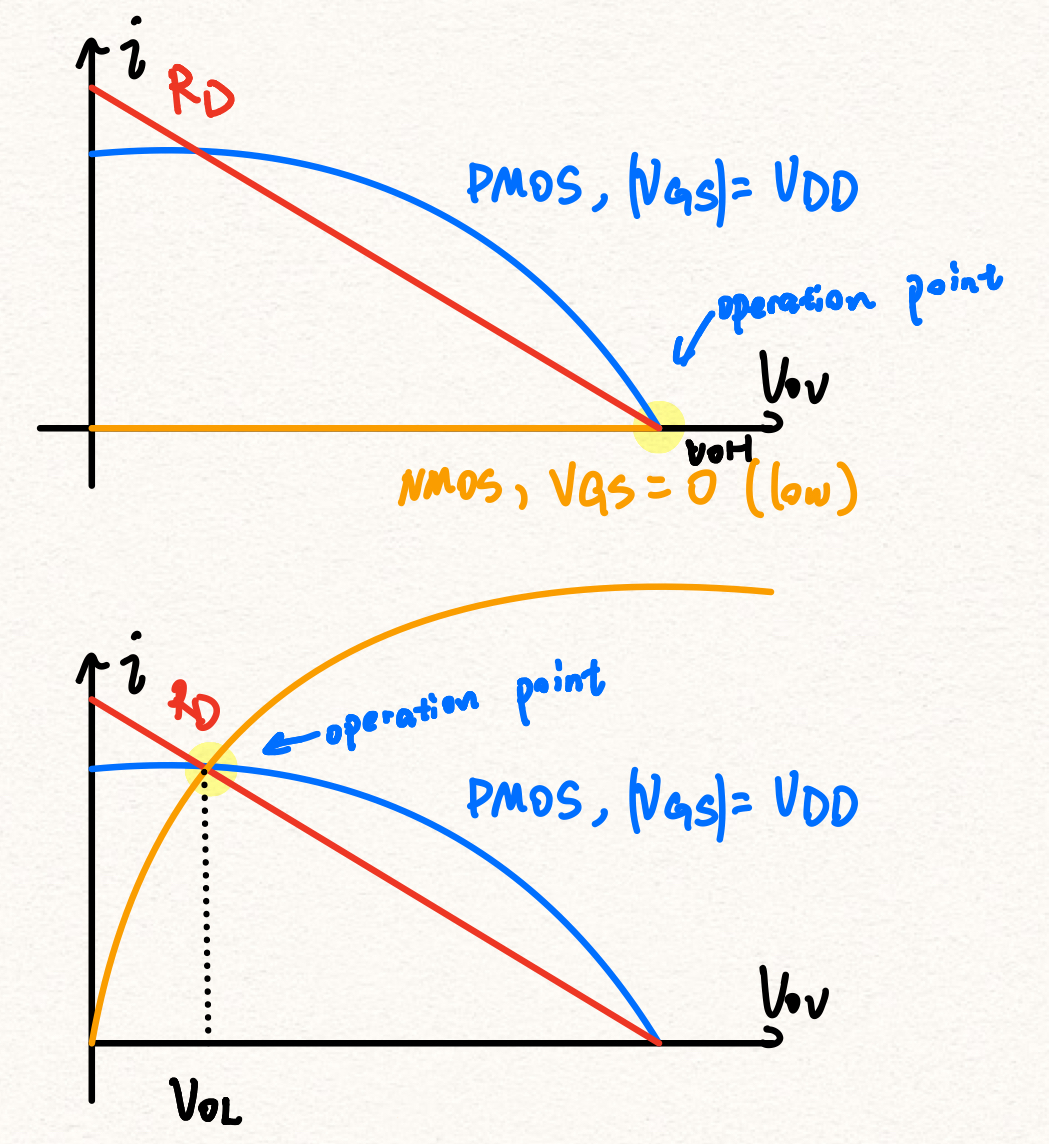
CMOS Inverter
无论怎么调整,只有一个MOS的inverter终究会遇到问题,要么是
于是CMOS Inverter横空出世
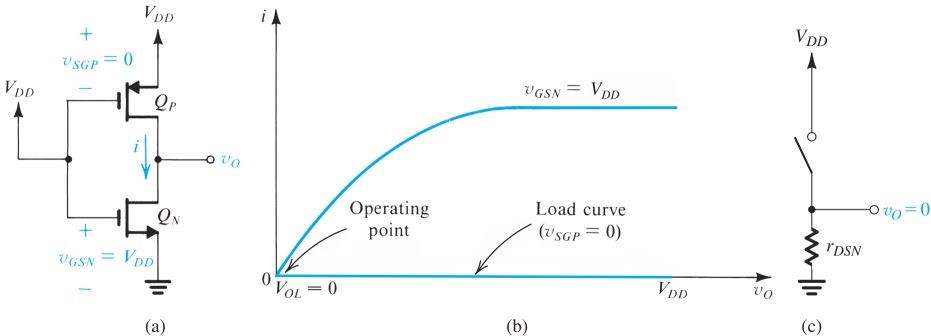
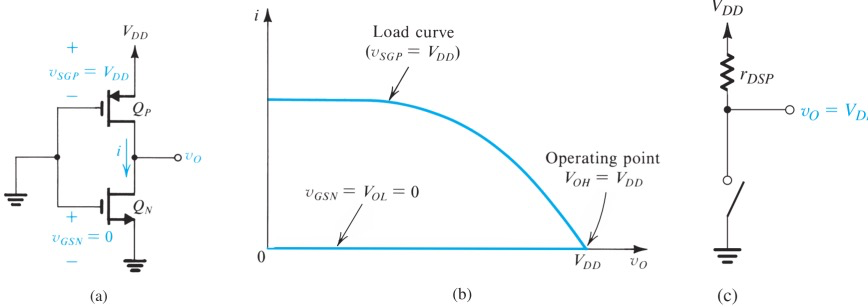
假设load的current不是很大,那么两种情况下导通的那个MOS管都工作在Triode region,于是等效电阻:
(即使不是,在saturation region所能到的驱动电流也不小)
一些CMOS Inverter的特性
Static power dissipation = 0,如果不计leakage current,那么在high与low状态没有任何电流通过,后面会分析switching power
Input resistense is infinite, inverter can drive an arbitarily large number of similar inverters with no loss in signal level
output resistance is low (low output resistance -> less sensitive to noise and other disturbances)(why?)
Output voltage level 0~VDD,最大化voltage swing,同时也可以最大化noise margin
VTC of CMOS inverter
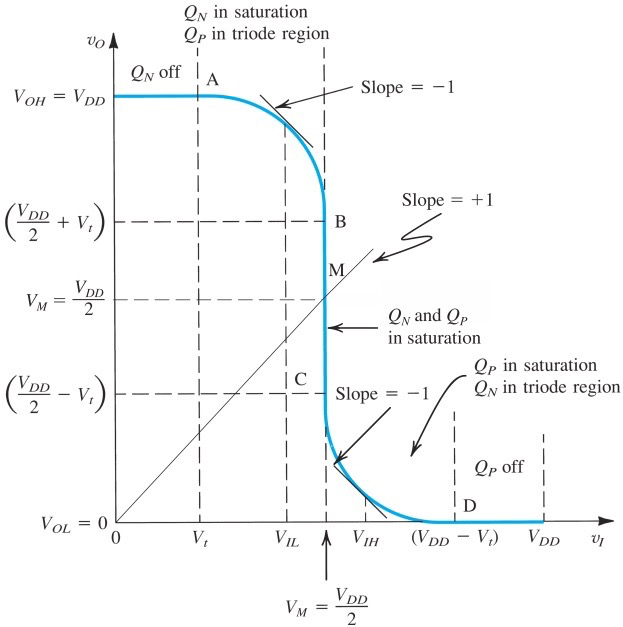
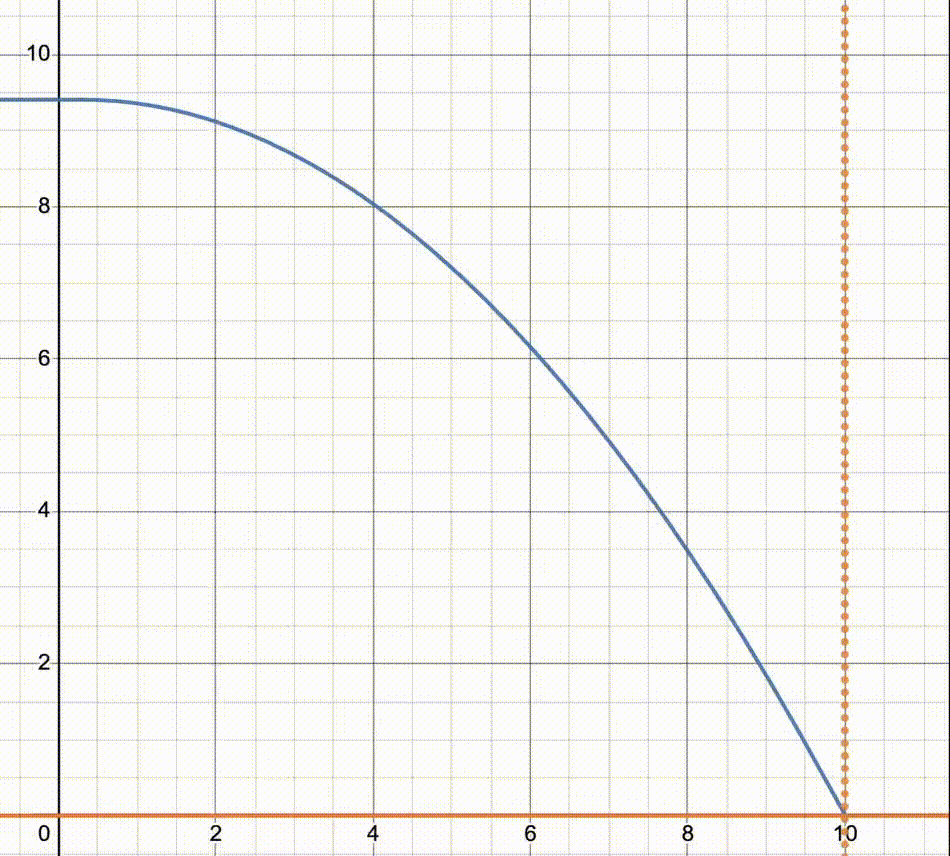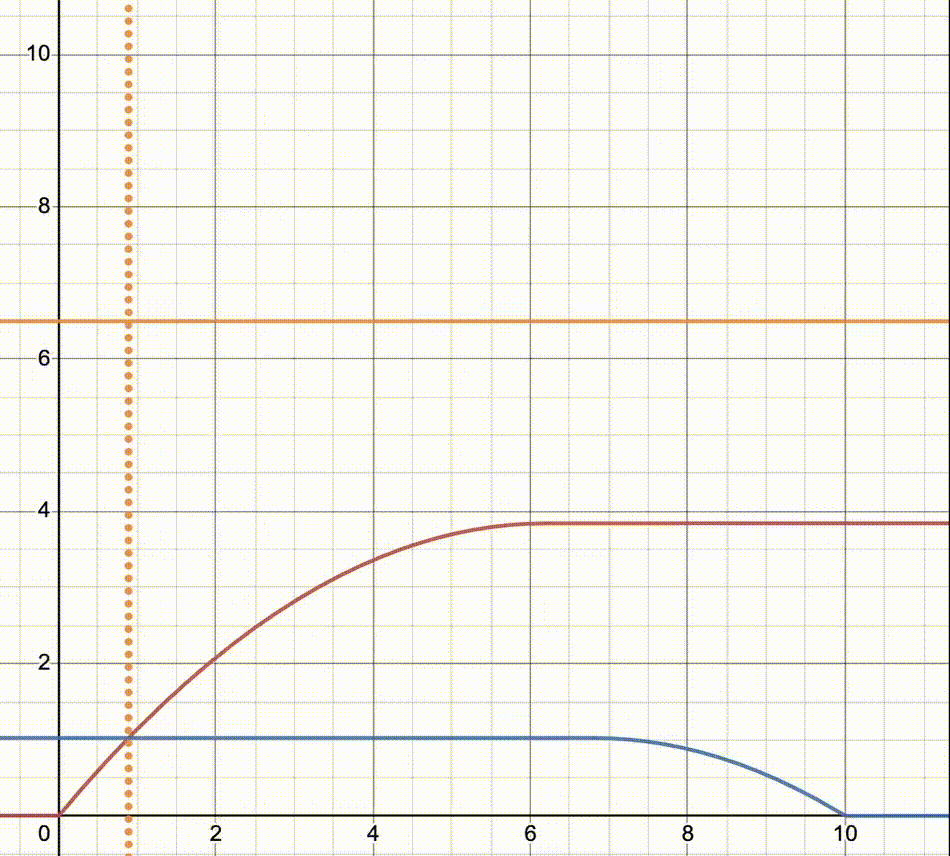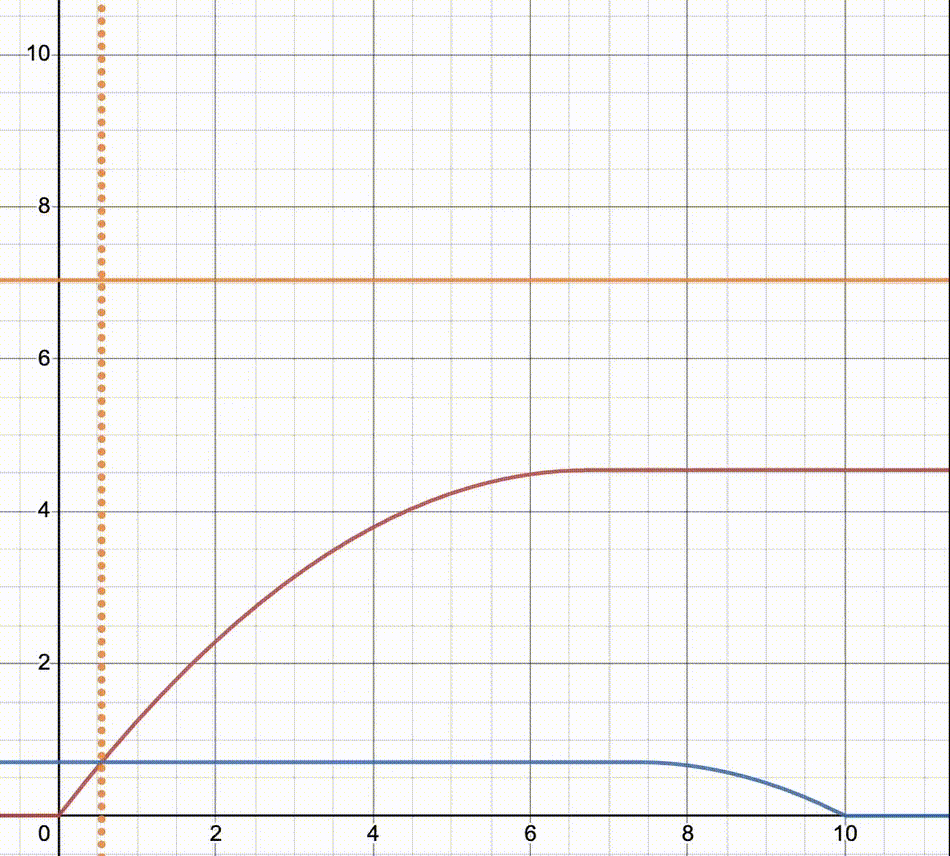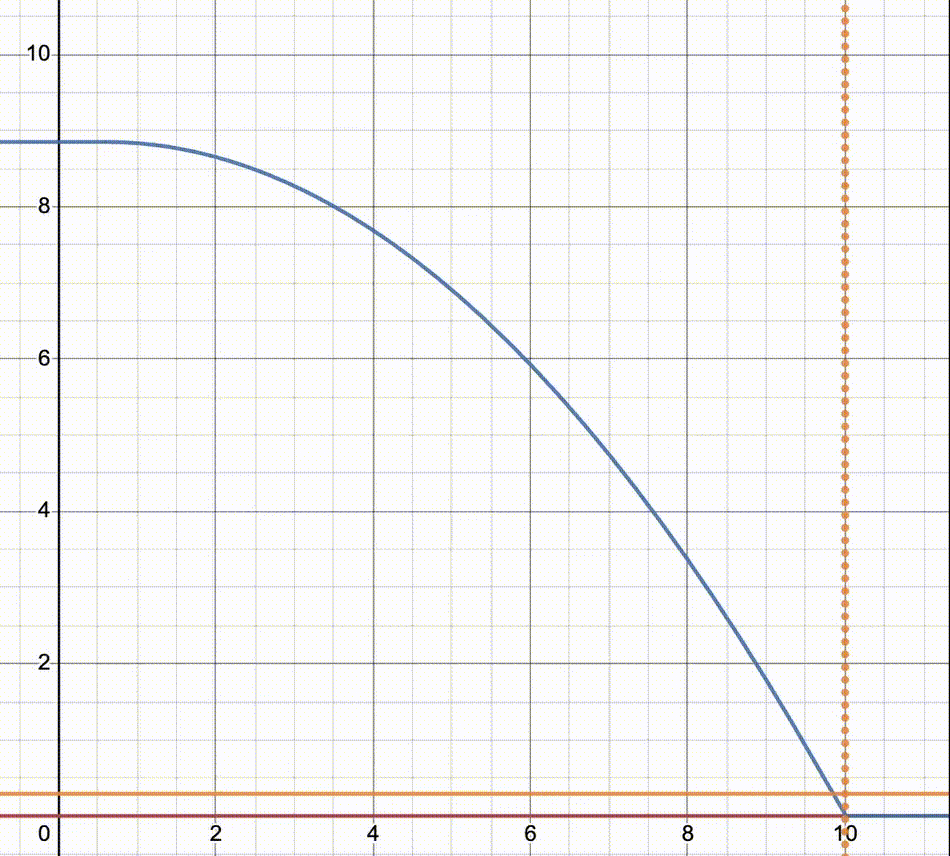
红色线是NMOS的load line,蓝色是PMOS的load line
横坐标
,纵坐标 注意橙色线的交点,横向的橙色实线代表
,所以右图中橙色交点构成的轨迹跟左图中心对称 动图可以比较直观的看出不同阶段两个MOSFET分别工作在哪种模式,二次函数的曲线就是triode,水平的就是saturation
找到
首先找到对应的区间,然后对方程进行differential by part
两边同时对
代入
假设
将这个带回到求导前的公式可得
这步我手推没推出来,但带回去确实没问题
那么可算
上面的desmos动图以及VTC都是assume
这样的代价则是PMOS所需面积变大,甚至导致寄生电容增大
我们可以计算
此时,代入M点电压特性
令
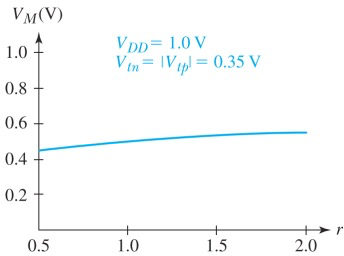
可以看到如果不对称的话,其实影响并不是很大(当然VTC曲线会变化),但是如果愿意接受
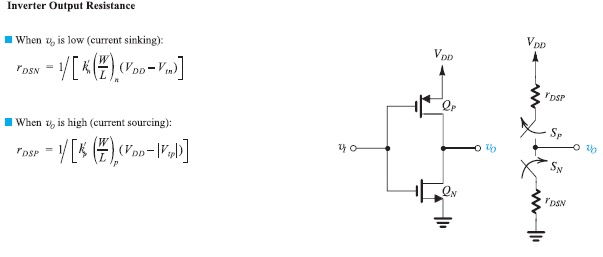
Dynamic Operation of CMOS Inverter
Propogation Delay
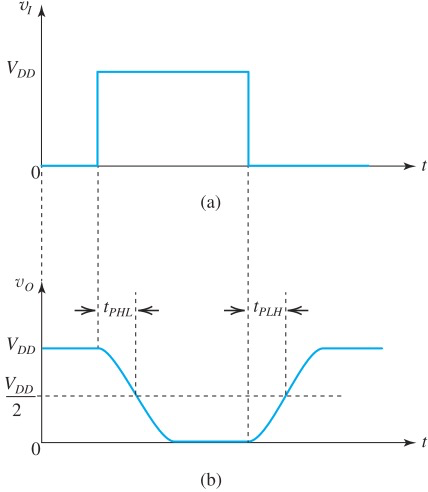
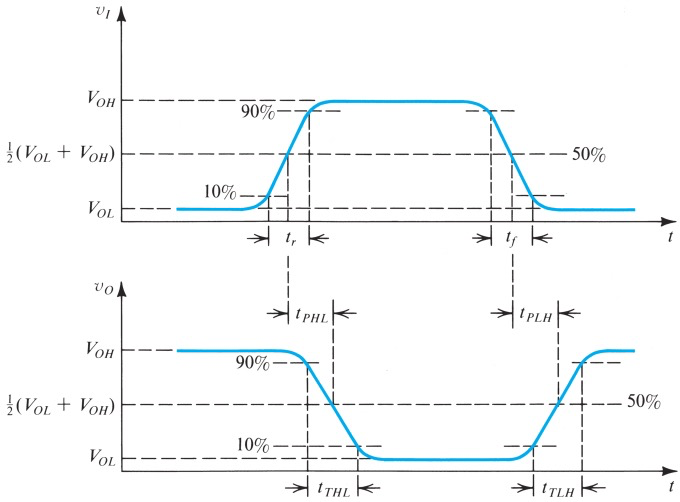
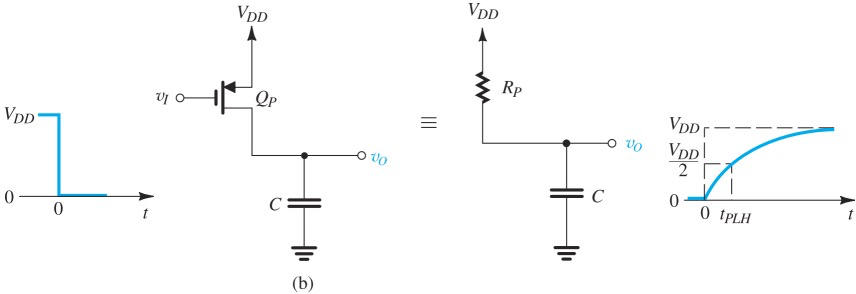
由于寄生电容的存在,每次切换CMOS状态时都相当于RC充电电路(后面会细说),这会导致延迟。因此
Propogation Delay:
分别代表在输入
并且定义
P - Propagation, T - Transition
HL - High to Low, LH - Low to High
通常Inverter的输入来自上级Inverter,因此输入往往也有rise and fall times
这样会产生额外的延迟,叫做Transition Times
这四个时间是输出
Step response
Calculation of Delay
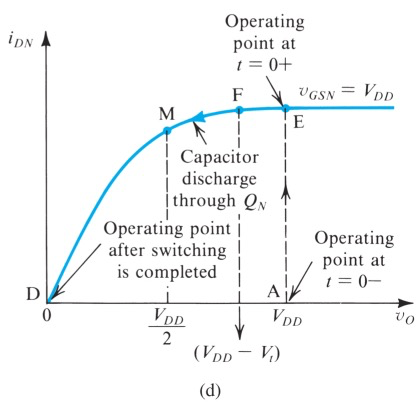
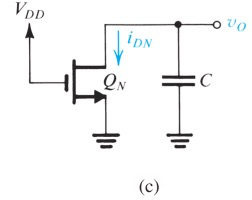
用Step response的方式来分析
最开始NMOS处于cutoff,t = 0时突然进入saturation。Vo 一直处于VDD (A点跳到E点)
NMOS开始导通,但由于还是saturation,电流恒定 (E到F)
直到由于电容的放电,Vo(就是
从此开始进入Triode放电模式 (F到M)
可以看到,两边其实都是first order differential equation,可以通过求积分的方式得到t
不过得到的公式也很复杂,因此我们引入一个approximation - 整个电容放电的电流恒定为
代入
根据电荷守恒有
这样
同理,
上升沿和下降沿时间match的条件是
尽管时间跟
是负相关的,但无论是通过 降低还是(W/L)降低都会增加C,所以要优化出合适的 值
Velocity Saturation Effect
在实际制造中,velocity saturation effect会导致实际流过的电流比理论上小,因此可以用另一种方式来估算时间
这在某种程度上简化了我们的分析,因为一般即使在triode region的M点理论电流也会受到影响,因此整个放电过程可以将PMOS和NMOS等效成电阻变成RC电路

根据电路,
同理,
而
Ramp-input Voltage
上面的两种分析输入都是方波,而实际应用中,正如之前说的一样,Inverter的输入通常来自另一个Inverter,因此也有上升沿。这会导致电容开始放电时,电路并不是像我们分析的一样完全断开的,而是两个MOS都会参与。因此有经验公式
Capacitance of CMOS
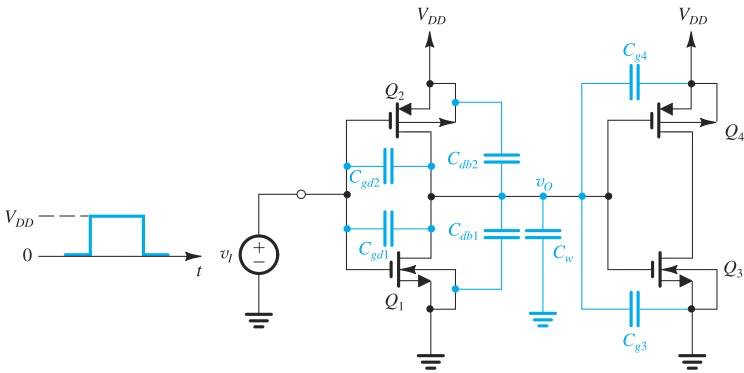
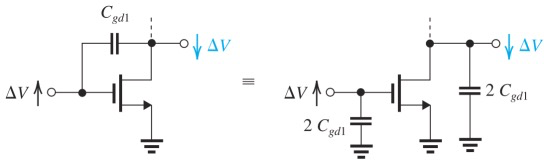
对
因此
连接到
的 也可以等效成接地的,因为我们输出只在 与0变化,所以只是充放电状态相反,其它完全相同
通常,我们让fanout of 4来定义一个technology的Typical Delay,也就是输出会接到4个其它的Inverter上
米勒效应 S&S 10.2.5
上图是Miller Equivalent Circuit
我们假设Node1和Node2链接电路的其他部分,而
这时,我们可以将Impedeance Z等效成两个分别对地的Impedeance,值如图所示
在我们这个MOS电路中,当切换状态时,
上升 , 下降 ,相当于电容两端电压变化了 。因此Miller equivalent的K=2
Transistor Sizing
Inverter大小取决于transistor的大小,而transistor的大小与
定量分析Aspect Ratio对
当我们把aspect ratio 增大S倍,internal capacitance增加S倍
对于MOSFET Velocity Saturation 导致的内阻,我们用equivalent resistance
这样,
当aspect ratio 增大S倍时,内阻减小
由此可见,aspect ratio的增大不影响内部电容对tp的影响,而是会弱化外部电容对tp的影响影响,设计时需权衡S增大导致的面积增长
等效 Aspect Ratio
等效aspect ratio可以像电容一样在电路中被计算出来,通常,我们设计Inverter时的思路是等效PDN aspect ratio与最基础的inverter的aspect ratio相同,PUN也是 (worst-case gate delay equal to that of the basic inverter)
同理,
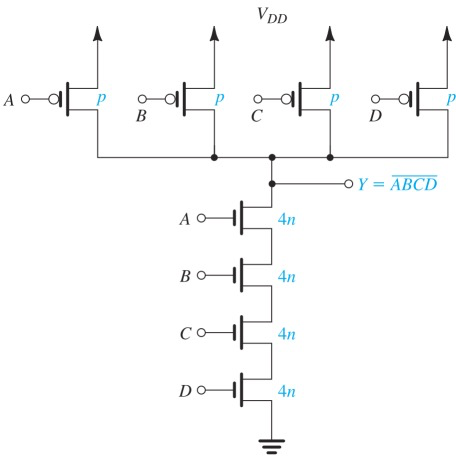
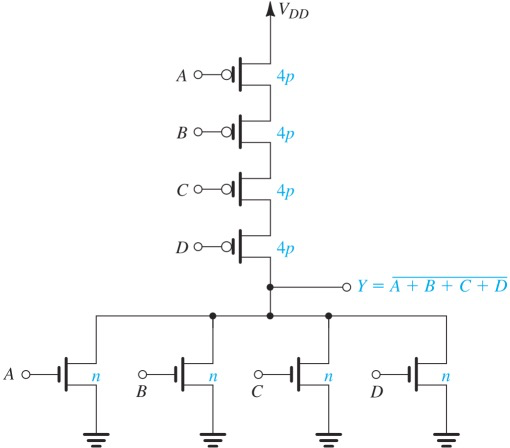
可以看到,NAND Gate(左)每个NMOS都要4n的aspect ratio,而对于NOR Gate(右),每个PMOS要4p
考虑到通常制作工艺下,PMOS的aspect ratio要大一些(因为空穴导电能力没有电子强,
因此,NAND Gate比NOR更省空间
NAND Gate下面每个都是4n,因为当电流流过时,
压降被4个MOS平均分压,因此电流更小了。要记得等效aspect ratio是由Velocity saturation导致的电阻计算的
Fan-in and Fan-out
正如上面对电容进行的分析,更多的Fan-in和Fan-out会导致Transistor的增多,进而增加等效电容C。因此一般过多的fan-in会在设计过程中被factor out
Driving Large Capacitance
当要很强的驱动能力时,我们需要更小的电阻,但单纯的增加aspect ratio增加面积会导致电容增大很多,使控制电路延迟增大
因此我们使用逐渐变大的Inverter Chain,这样既能隔离开驱动带来的影响,也能达到更快的速度
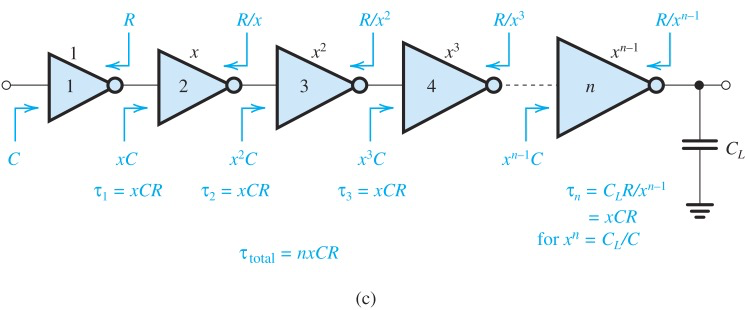
如图所示,这个chain中,每个inverter的aspect ratio是上一个的x倍,因此每两个inverter之间的
当我们最后一级(最大的,实际驱动的Inverter)的
数学上可以证明,当delay最小时,
假如你只用两层,其实也算是chain,只不过可能会得到不是很好的x值,但只要用了,就会让最左侧的控制信号感受到最小的电容,实现某种程度的隔离
Power Dissipation
Static Power Dissipation - Power dissipation when the inverter is not switching
Dynamic Power Dissipation - Power dissipation when inverter switches states
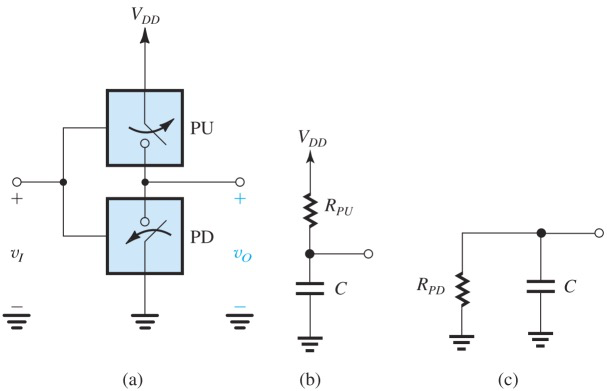
将RC电路看成一个整体,
由于电容储能
因此
充电放电都是相同的公式,因此一个完整的周期,
还有另一部分dynamic power,来自直接流过两个MOSFET的电流。设想在
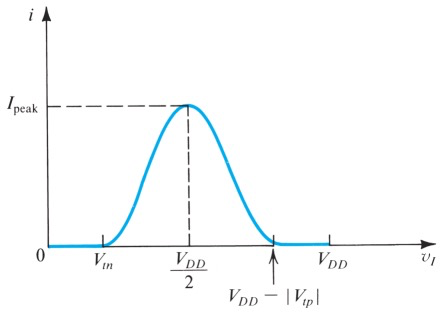
这个图像可以参考上次的动图,新加了两条绿线表示
https://www.desmos.com/calculator/trjng25kd4
PDP & EDP
Power-delay product -
当inverter工作在最大频率下(正弦波)时,
Physical interpretation - energy consumed by the inverter for each output transition
不过由于PDP的表达式没有
Energy-delay product -
参考: stm32 GPIO的三种频率模式,越低的频率功耗越低
Deep-Submicron Design
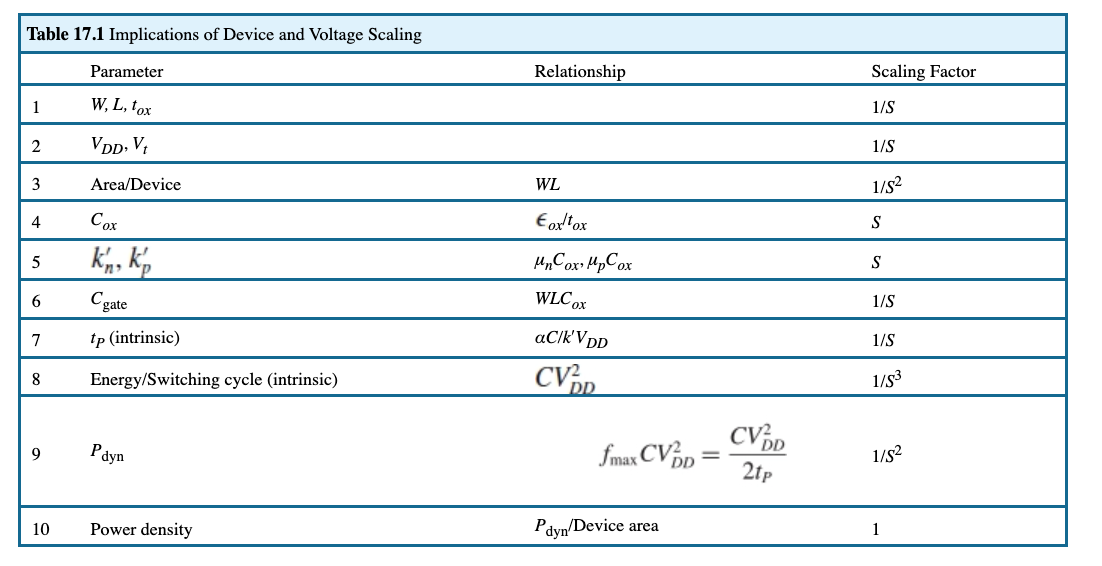
一个更全的Scaling的图
当把MOS做的更小时,Leakage Current会增大,之前提到交sub-threhold condition,会导致更大的功耗。温度更高时,
很多时候芯片为了省电会直接关停某一整片不用的区域,那片区域的Capacitance不再产生功耗,叫做Power Gating。用于控制关断的开关MOS使用Multi-Vt technolgy实现low leakage。