寻找最少回文串插入字符
给定任意一个长度为n的字符串(n<=10),可以向其中任意位置插入字符,使其变成回文串,如"banana"可以在最右边插入一个‘b’而变成回文串,因此f(“banana”) = 1
分析
这个题最主要的就是找到递归的方式,我最开始掉到坑中去了,想找里面的最长回文子串,然后对两边分类讨论,后来发现这样写出的算法过于复杂且难以实现。
正当一筹莫展的时候,一个“banana"突然启发了我,如果每次只看开头和末尾的字符,如果相同,就继续向里面看,如果不同的话,把左边的补到右边去,然后再对里面剩下的做同样的操作就完成了 - 比如abacca只要在右边+ba。
但有一个问题,在右边插入字符不总是最好的方案,abacc最好的方案是在左边+cc,而不是在右边+aba
递归中神奇的一个min
解决这个问题,只要两种方法都尝试一下就好了,而这个时候,就需要你不要去想整体,而专注与小问题。
这个递归函数的原理就是给定了一个字符串“a{str}b”,其中{str}是任意长度字符串,而a和b都代表单个字符
首先去想a==b的情况
假设这个X是个回文串,那么aXb就直接是回文串了,所以不需要插入数字,return 0
那如果X不是回文串,我们可以通过插入的方式把它变成回文串,只需要插入f(X)个字符就可以了
所以,这种情况下,f(aXb) 是等于f(X)的
a!=b的情况
这种方式,你可以在右边插入一个a,变成f(aXba),那么就回到了上一个情况,因此f(aXba) = f(Xb)
或者在左边插入一个b,变成f(baXb) = f(aX)
那么f(aXba) 和f(baXb)有什么用?
aXba是aXb插入一个字符得到的,baXb同理,因此f(aXb) = f(aXba) + 1, f(aXb) = f(baXb) + 1
但是f(aXba)跟f(baXb)未必相同,由于我们在找最少的量,所以两个取一个min()就好了
f(aXb) = min( f(aXba) + f(baXb) ) + 1 = min( f(Xb) + f(aX) ) + 1
到这里,我们已经成功的把一个大问题能够拆成小问题了,那么可以写出递归了
不过在递归之前,先处理一下base case
其实一共就两种base case,一种是X为空字符串,另一种是X只有一个字符 (len(X) == 0, len(X) ==1)
这两种情况,是没法凑成aXb的。不过这两种情况本身都可以看作回文串,所以直接return 0
至此,这道题最难的部分已经结束了
三行代码,递归就写出来了
fn insert_pal_rec<T: std::cmp::PartialEq>(arr: &[T], start: usize, end: usize) -> usize{
if end <= start { return 0; }
if arr[start] == arr[end]{ return insert_pal_rec(&arr, start+1, end-1); }
else{ return std::cmp::min(insert_pal_rec(&arr, start+1, end), insert_pal_rec(&arr, start, end-1)) + 1; }
}
这个代码可以解决问题,但还能有更多优化的空间,而优化的部分也是我写这篇博客的主要动力所在,所以如果感兴趣的话可以继续看下去
前方高能,完全看懂需要对big O notation的了解
但如果你只想看思路,并且感受一下算法的魅力,没有这些知识也无所谓,不要在没看懂的地方纠结太久就好
[题外话]返回值怎么传?递归一去一回的思想
在看我同学的代码时候,发现有人写递归的时候多传了一个参数ret,用来记录返回值,像这样
import math
def process( str, ret ):
if base_case: return ret
return process( str[1:-1], ret ) if str[0] == str[-1] \
else math.min( process(str[1:], ret+1), process(str[:-1], ret+1) )
为了探究到底哪种更好,我特地学了汇编,看了下编译后的代码,参考这篇文章“递归返回值该怎么传?- 让我康康你的汇编!"
代码很短,但效率如何?
仔细分析一下这个代码,不难看出时间复杂度是O(2^n^), 空间复杂度是O(n)
时间:最差情况下,对str的每个字符都要去试着从左边加和从右边加,因此每个字符都有插入左边,“插入右边”,两种可能
递归过程中只用传两个变量,所以是常数大小,而递归的深度最差情况是n-1次,因为每次都少一个字符,直到剩1个
如果在递归过程中clone了一个str传进去,那么每次传值的内存占用就变成O(n)级别了,总体就变成O(n^2^)了
指数级别的时间复杂度是很可怕的,现在再看就明白为什么限制n<=10了,即便我用rust写的代码,也没法用这种方式解决n=30长度的字符串
为什么这么慢? - 相同的活重复干了很多次
假如我们现在想要求的字符串是"kcabad"
那么可以画出来这个图:
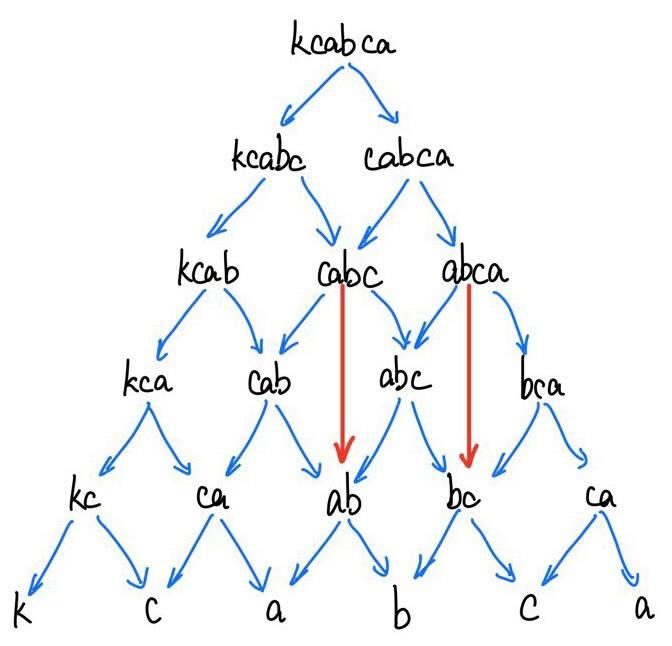
可以看到,f(kcabc)与f(cabca)都需要f(cabc)的数字,而这就导致f(cabc)被执行了2次。f(ab)更惨,要被调用4次。不过很明显,f(cabc)返回的结果跟之前的选择无关(无论是谁管它要数据,它都会返回相同的结果,前面的选择“没有后效性”)
于是我们有了一个思路,如果能够缓存函数的返回值,让每个函数只会执行一次,这样就能剩下一大笔时间,拿到一个时间复杂度为O(n^2)的算法。这个缓存的思想,便是动态规划 - Dynamic Programming。
记忆表索引 - 无脑空间换时间
再次小分析一下,我们之前写的递归一共传了3个值,字符串,字符串开始位置,字符串结束位置。
这个字符串是一直不变的传下去的,因此,(start, end) 两个值决定着函数的返回值,换句话说,f()是只跟start,end有关的函数。
那么只要稍微修改一下之前的递归,用一个二维矩阵保存所有的结果,就可以让速度得到极大提升
fn insert_pal_map<T: std::cmp::PartialEq>(arr: &[T]) -> usize{
let mut map: Vec<Vec<Option<usize>>> = vec![vec![None; arr.len()]; arr.len()]; //初始化二维数组
return process_with_map(&arr, 0, arr.len()-1, &mut map);
}
fn process_with_map<T: std::cmp::PartialEq>(arr: &[T], start: usize, end: usize, mut map: &mut Vec<Vec<Option<usize>>> ) -> usize{
//跟之前一样,只不过每次先看一下缓存中有没有结果,如果缓存命中,直接返回,否则计算后,放入缓存,再返回
if end <= start { return 0; }
if map[start][end] != None { return map[start][end].unwrap(); }
let ret: usize;
if arr[start] == arr[end] {
ret = process_with_map(&arr, start+1, end-1, &mut map);
map[start][end] = Some(ret);
}else{
ret = std::cmp::min(process_with_map(&arr, start, end-1, &mut map),
process_with_map(&arr, start+1, end, &mut map) ) + 1;
map[start][end] = Some(ret);
}
return ret;
}
这个算法,时间是O(n^2^),而空间是O(n^2^) (不过注意递归造成的空间复杂度还是O(n),不过复杂度只找最高次项)
整理一下思绪 - 严格表结构登场
可以发现原来的问题,可以看作在这个树中找到从最顶部到最底部最短的距离。
而当两个字符串相等时,相当于为这条路抄了个近路,跳过了一层。因此,哪条路跳过的最多,代表利用了更多原字符串中相同的字符,进而插入的数量越少。
那么再看一下最后一行,刚好是原字符串的每个字符拆开来。那么我有一个大胆的想法,能不能直接从最下面出发,不递归了,而是一层一层叠上去,求得最后的值?
那么我们可以画这么一个矩阵,用这个矩阵来求"kcabca"的最小插入字符数:
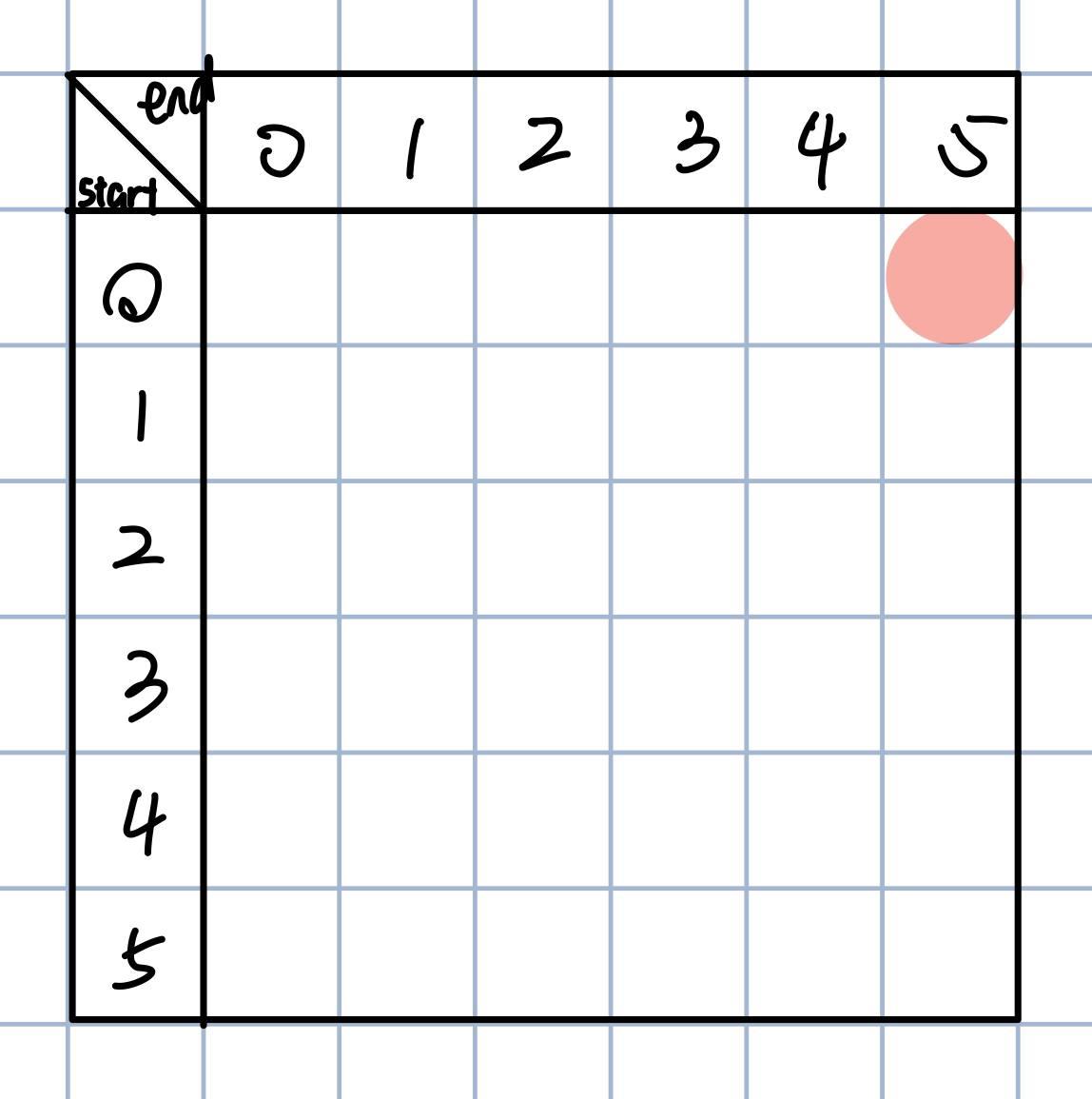
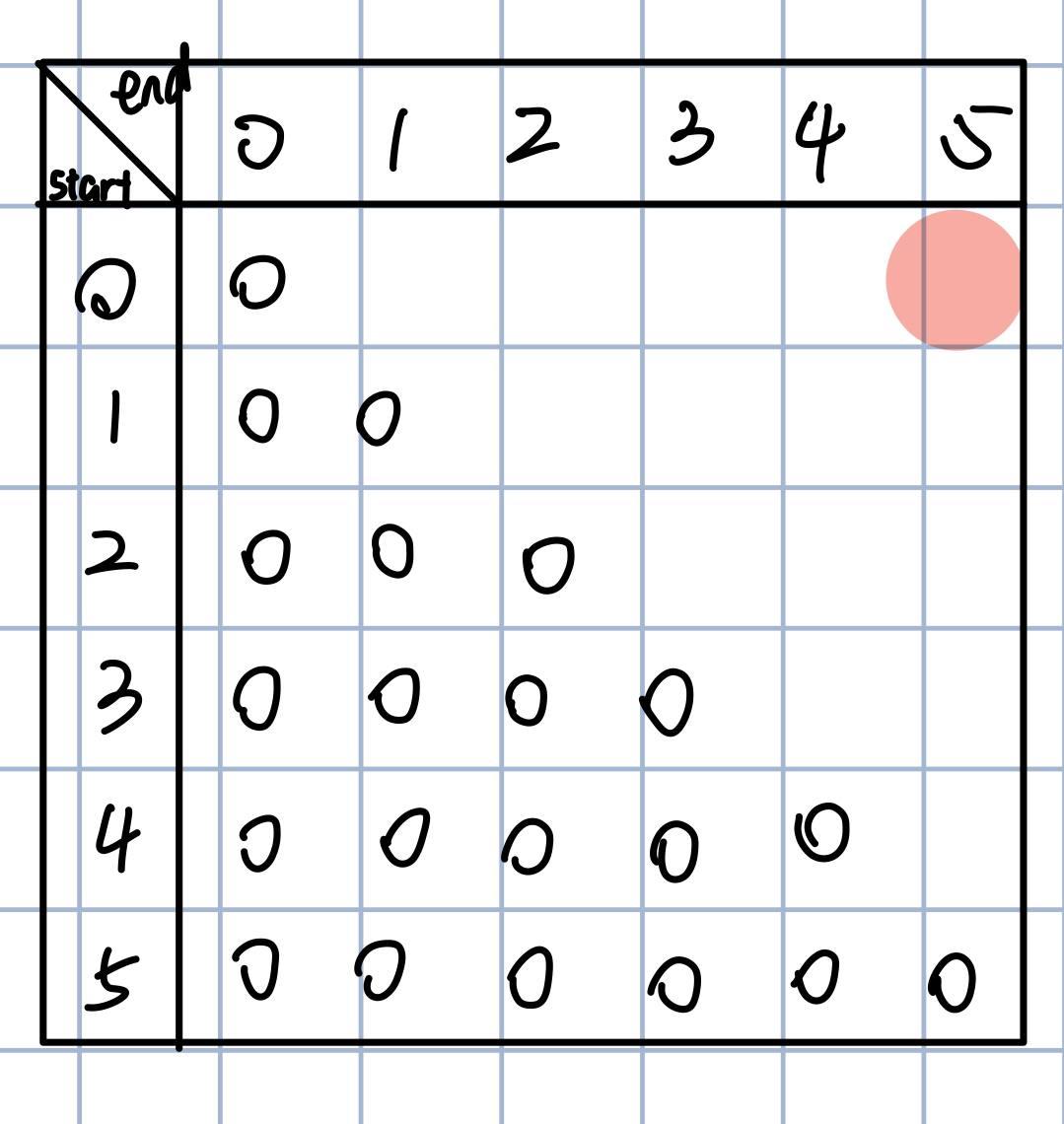
每一行代表一个开始位置,每一列代表结束位置,我们最终想要的是start=0, end=5的位置,也就是右上角,那么下面就是按照我们的规则填好这个矩阵
根据我们递归的base case,当end<= start时,返回0
递归中的下一步就是判断是否相等,我们对这里还没填的格子也这样做,如果str[start] == str[end],就标红
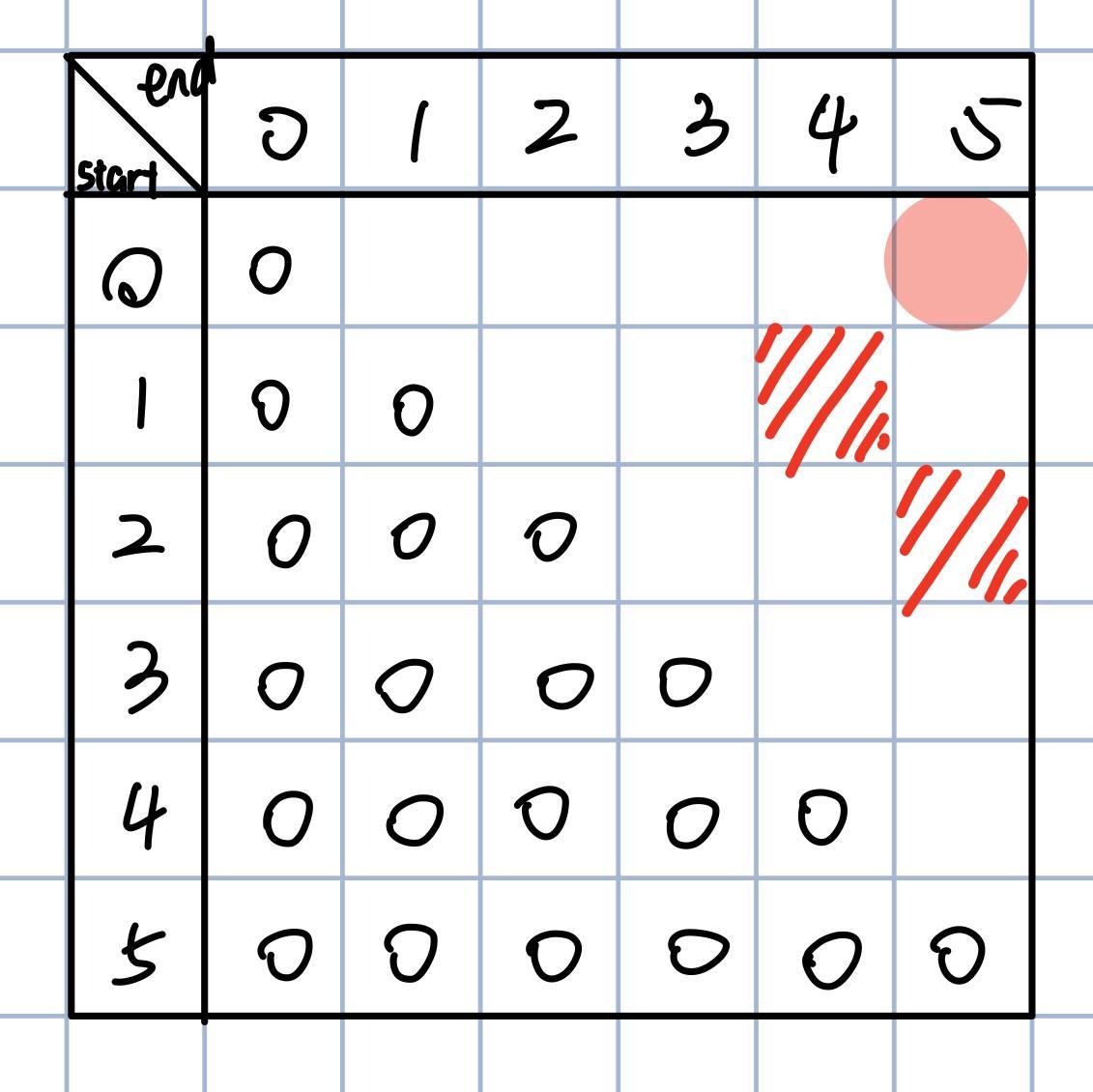
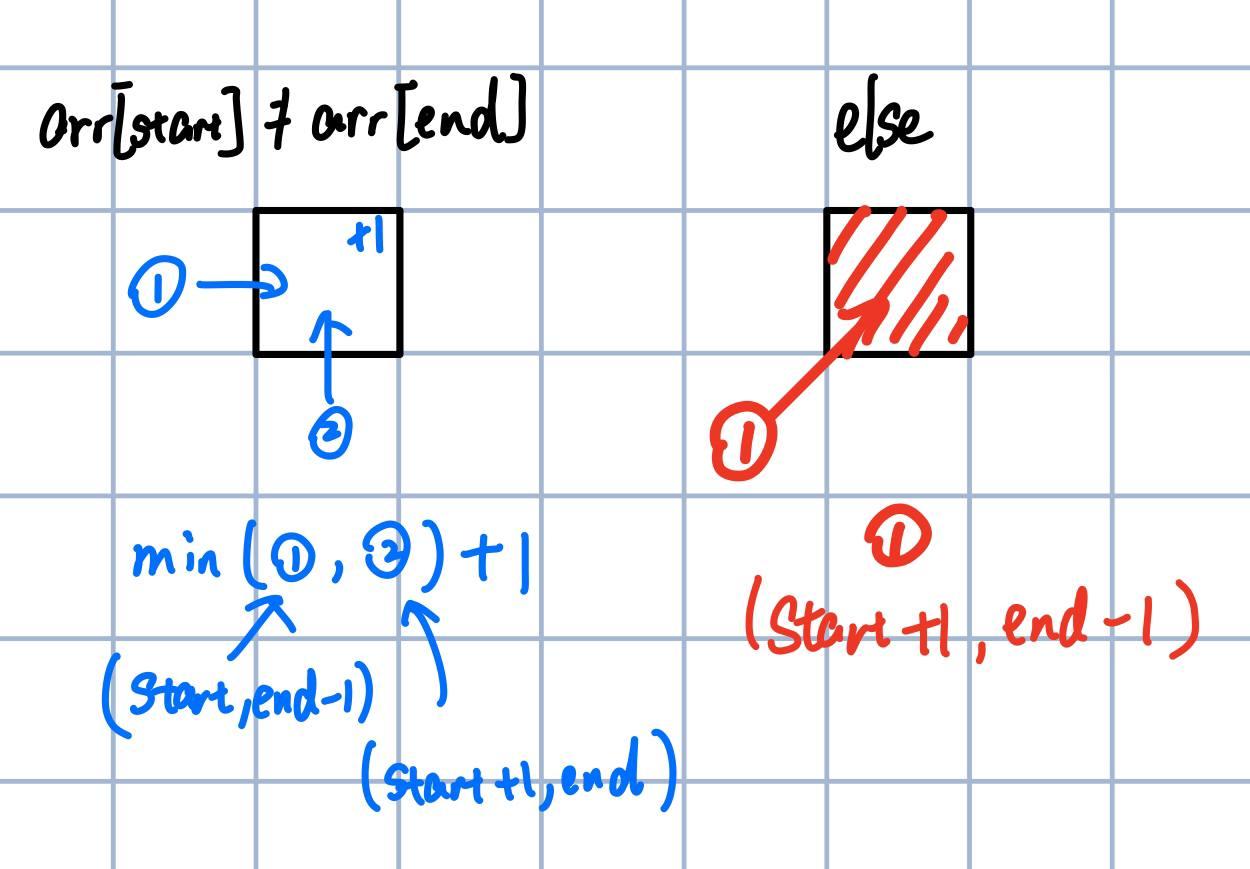
记得刚才的分析,如果两个字符相等,相当于抄了一条近道,这一点再这个矩阵中也能体现出来。上面右边的图就是矩阵中每个格子的填入规则。如果相等,那么直接去拿左下方的值。如果不等,那就从左边和下边取最小值,然后+1
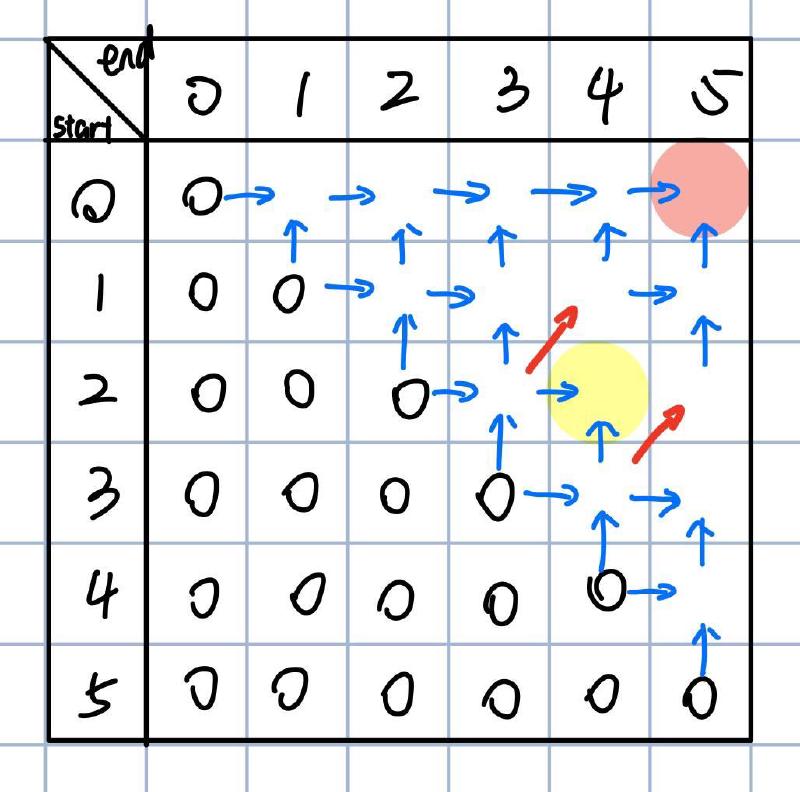
于是我们可以根据上一步的两张图,画出来如下的各个格子的关系图:
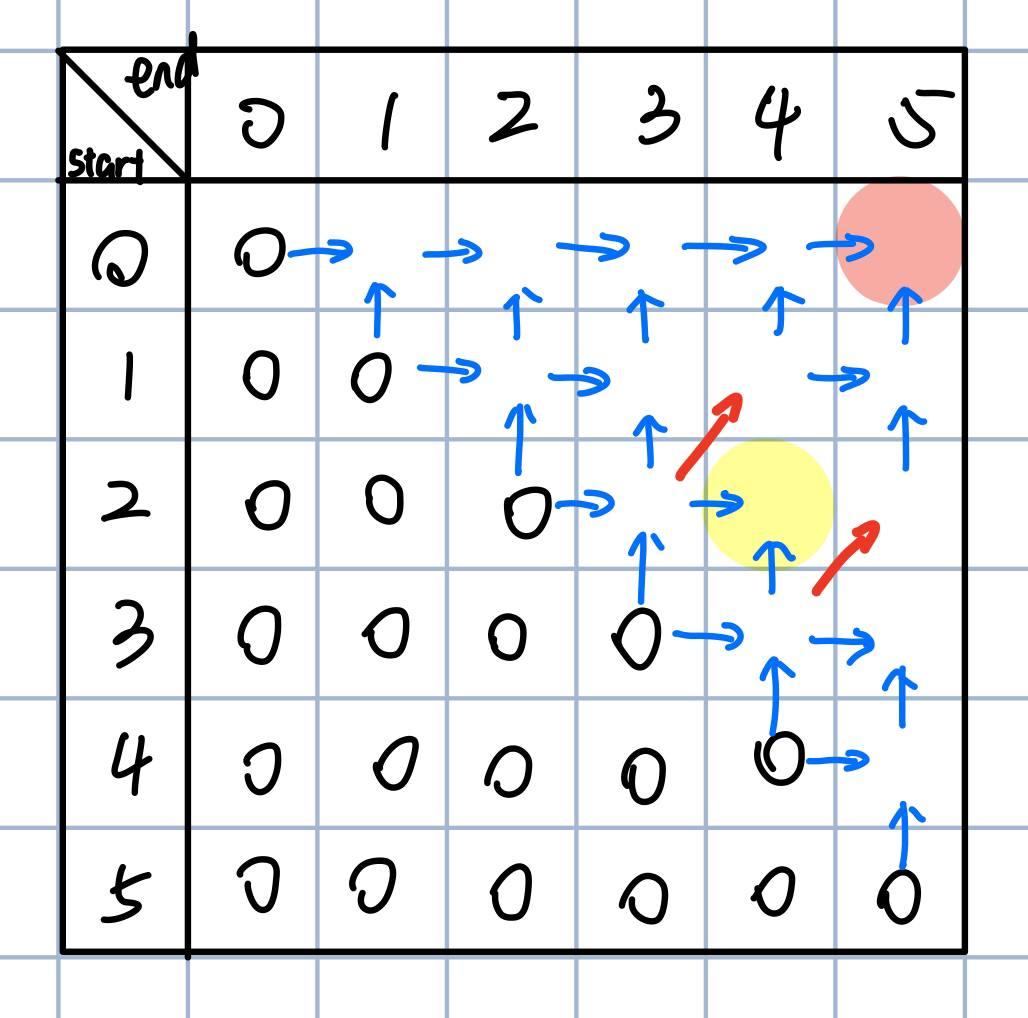
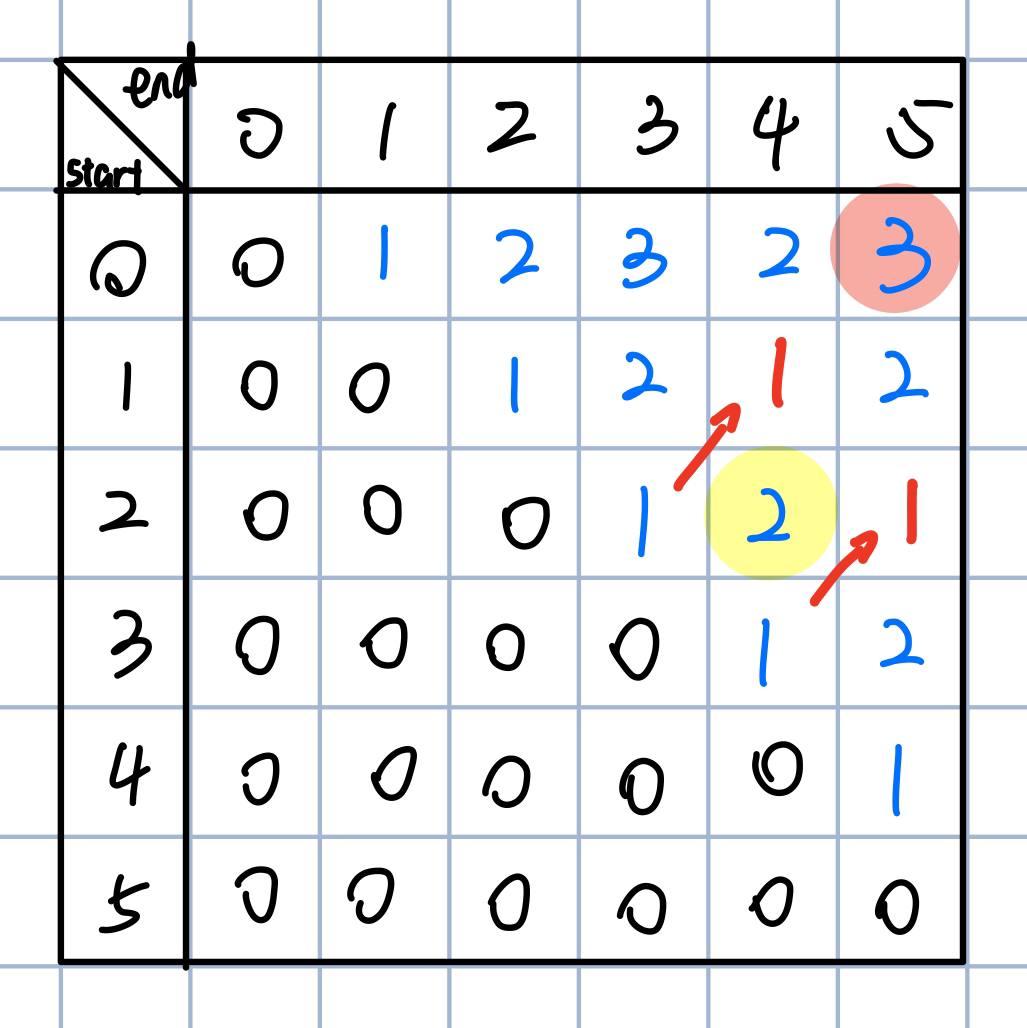
画完关系图就可以直接把矩阵填好了,所以最后的结果是3
代码实现如下:
fn insert_pal_table<T: std::cmp::PartialEq>( arr: &[T] ) -> usize{
if arr.len() < 2 { return 0; }
let mut table: Vec<Vec<usize>> = vec![vec![0; arr.len()]; arr.len()];
for diff in 1..arr.len(){
let mut i: usize = 0;
while i + diff < arr.len() {
if arr[i] == arr[i+diff]{
table[i][i+diff] = table[i+1][i+diff-1];
}else{
table[i][i+diff] = std::cmp::min(table[i][i+diff-1], table[i+1][i+diff]) + 1;
}
i += 1;
}
}
return table[0][arr.len()-1];
}
分析一下这种方法之后发现时间复杂度还是O(n^2),空间复杂度也是O(n^2),跟刚才无脑记录下来每个结果是一样的…
所以严格表结构有什么用?难道我们白忙活了?
首先,它的常数项少一点,系统不用去频繁的对记忆表进行读写操作,也不用去维护递归栈,速度就会快一些
其次,它能进一步进行优化…
能不能再省一点?! - 把这个算法彻底写成我看不懂的样子
刚刚的算法之所以是O(n^2^)的空间复杂度,是因为要记录下来整个n*n矩阵的值,但是我们似乎不需要那么多值,每个值用完后其实就可以丢掉了。
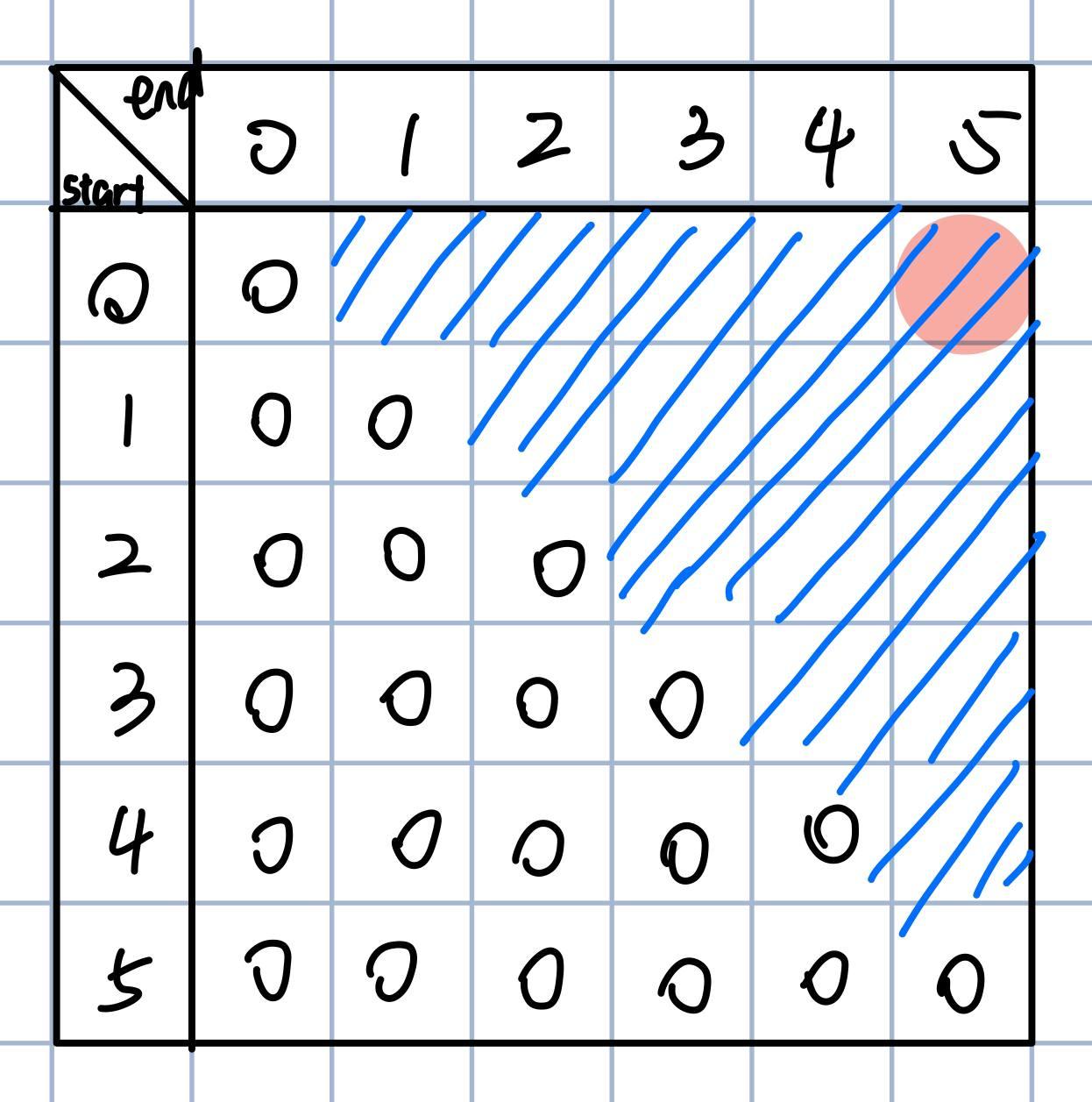
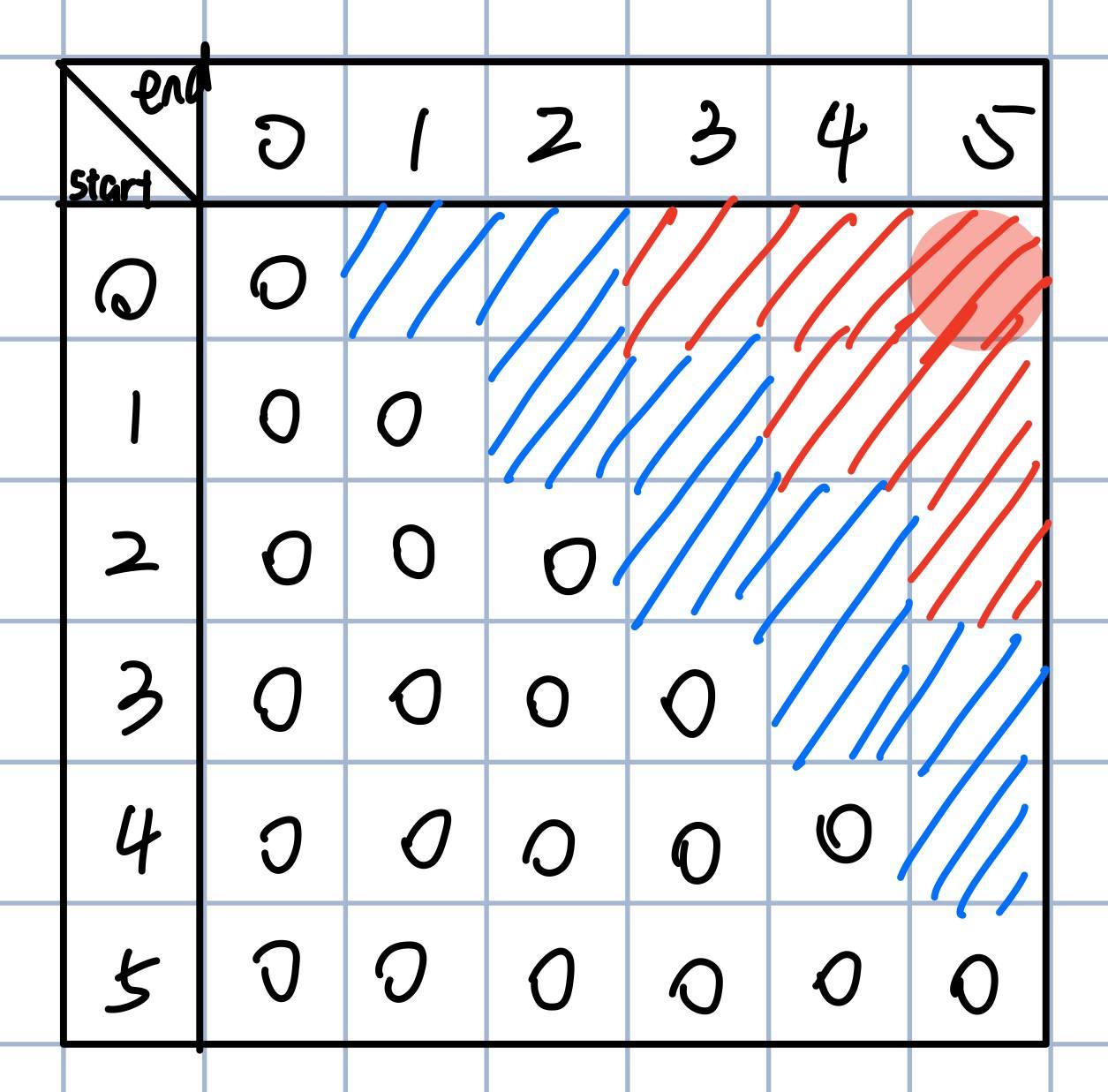
我们每次计算一个格子是,只需要它之前2条斜线上的数据。而距离整个矩阵斜线最近的两条斜线包含了2*str.len()-3项,而不难发现,用这么多的格子,完全可以把以后需要的内存空间涵盖进去。换句话说,这是我们将要用到的最大内存空间。
代码实现
fn insert_pal_table_mem_opt<T: std::cmp::PartialEq>( arr:&[T] ) -> usize{
if arr.len() < 2 { return 0; }
let mut temp: Vec<usize> = vec![0; 2*arr.len() - 3];
let diff: usize = arr.len(); //First data: 0..arr.len()-3, Second data: arr.len()-2..2*arr.len()-3
for i in 0..arr.len()-1{
temp[i+arr.len()-2] = 1 - (arr[i] == arr[i+1]) as usize;
}
for i in 2..arr.len() {
for j in 0..arr.len()-i{
if arr[j] == arr[j+i]{
temp[ (i%2)*(arr.len()-2) + j ] = temp[ (i%2)*(arr.len()-2) + j + 1];
}else{
temp[ (i%2)*(arr.len()-2) + j ] = std::cmp::min(temp[ ((i%2)^1) * (arr.len()-2) + j], temp[ ((i%2)^1) * (arr.len()-2) + j + 1]) + 1;
}
}
}
return temp[ ((arr.len()-1)%2)*(arr.len()-2) ];
}
这段代码我自己能给撸出来,那一刻感觉我像个战神一样
这样的话,内存复杂度O(n)级别的算法就诞生了。时间复杂度是O(n^2^) ,不过之后的实际测试也能证明这个O(n^2^)的实际运行速度比上一个快一些,因为一维数组的寻址要比二维快。 所以,经过一顿操作之后,我们成功地把原来的递归(时间O(2^n^), 空间O(n))的算法,优化成了现在这样。
自己推一个动态规划公式
$F[s,e] = (arr[s]==arr[e]) * F[s+1, e-1] + (arr[s]!=arr[e]) * min(F[s+1, e], F[s, e-1])$
相当于一个if操作,如果arr[s]==arr[e]则返回F[s+1,e-1],反之返回后边的min(…)
要知道,这一切的一切都是从最开始的递归结构推出来的。其实,就算不说题目是什么,只给递归的代码,也完全可以优化成现在这个样子。所以,刷题的时候不要总专注与去背各种题目的公式,而是知道这个公式怎么来的,并且怎么用它。
之所以之前说递归的部分是最难的部分,是因为想到如何把这个问题划成小问题需要试出来,而一旦知道了递归的规则,优化的步骤都是固定的。简单讲,找到如何递归靠脑子,优化递归靠手。
公式可以直接写出来严格表结构的代码,而严格表结构也有多种优化方法,因此刷题的时候往往推到了严格表结构就可以收手了(假如自己知道这些优化套路的话)。不过这些优化技巧一定要会,毕竟有剑不用,和没有剑是两个完全不同的事情。
实际运行时间与空间分析
随机生成10000个固定长度的字符串,测试每种不同算法的用时(单位:微秒microseconds),没有做动态规划的递归不予比较
| 100字符(单位 microseconds) | min | 25th | med | 75th | max |
|---|---|---|---|---|---|
insert_pal_map |
68 | 72 | 76 | 94 | 193 |
insert_pal_table |
10 | 10 | 11 | 12 | 26 |
insert_pal_mem_opt |
6 | 6 | 6 | 6 | 14 |
| 1,000字符(单位 microseconds) | min | 25th | med | 75th | max |
|---|---|---|---|---|---|
insert_pal_map |
12,167 | 12,671 | 12,775 | 12,909 | 22,592 |
insert_pal_table |
2,535 | 2,707 | 2,817 | 2,923 | 5,036 |
insert_pal_mem_opt |
541 | 554 | 557 | 570 | 1,069 |
| 10,000字符(单位 microseconds) | min | 25th | med | 75th | max |
|---|---|---|---|---|---|
insert_pal_map |
1,167,935 | 1,176,727 | 1,187,388 | 1,223,231 | 1,645,885 |
insert_pal_table |
509,278 | 522,494 | 526,456 | 531,771 | 597,337 |
insert_pal_table_mem_opt |
53,285 | 53,705 | 54,543 | 54,835 | 69,375 |
是的,这个10,000字符的测试我用我可怜的i5 CPU跑了6个小时
100,000字符 - 只有insert_pal_table_mem_opt能够不溢出我的16G内存,速度大概5s/个
最后安利一下B站的算法课,我也是碰巧在这门课里面刚学到这些优化套路,然后付出实践一下,这篇文章就当是我自己的笔记了